尽管TenforFlow(tf)最主要的功能是进行深度学习,包括卷积神经网络(CNN),循环神经网络(RNN)和深度神经网络(DNN)等等。但是作为一个深度学习框架,其也提供了进行一般统计学习和优化的工具。前面(1, 2, 3, 4)我们已经介绍了tf的基本设置和各个命令的含义。下面我们使用一个例子来展示怎么使用tf来进行多元回归拟合数据。具体的说,用一个例子来说明怎么借助tf的Stochastic Gradient Descent做多项式回归。下面的动图展示了拟合函数的参数(回归系数)在tf经过多次迭代以后,拟合曲线渐渐逼近真实值的过程。
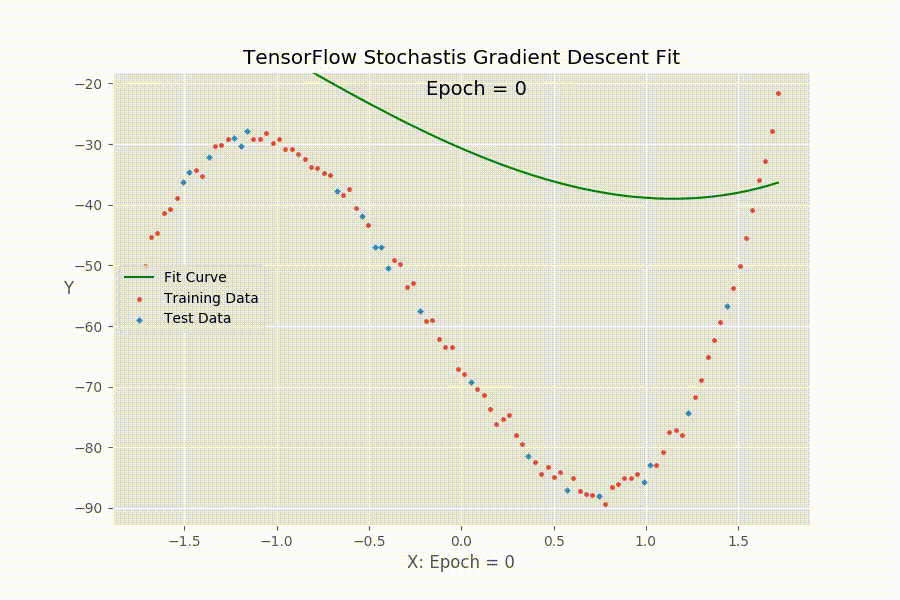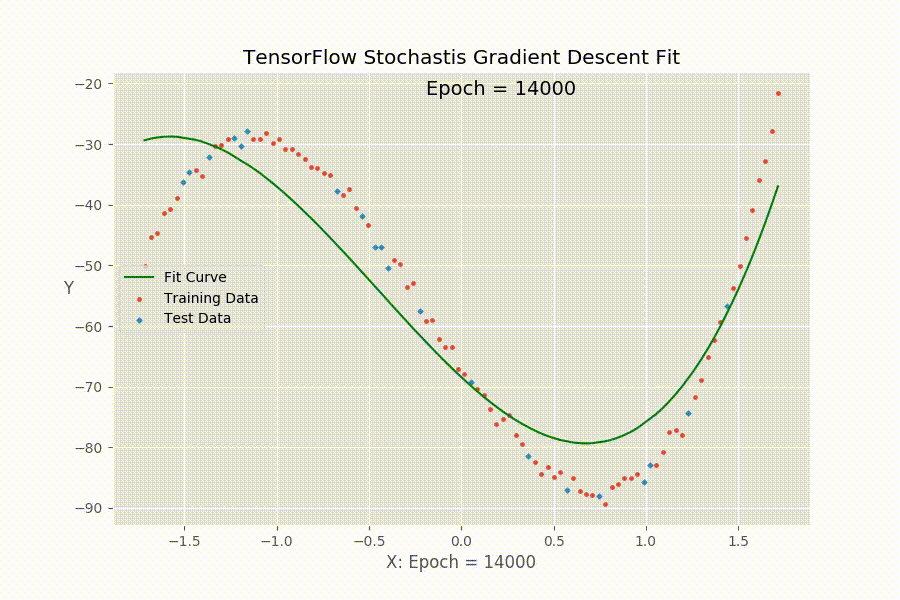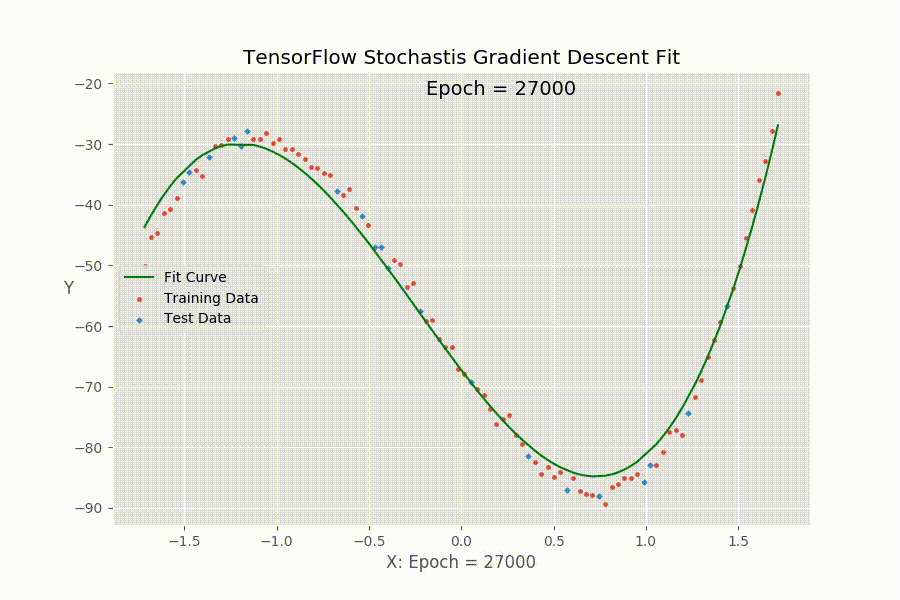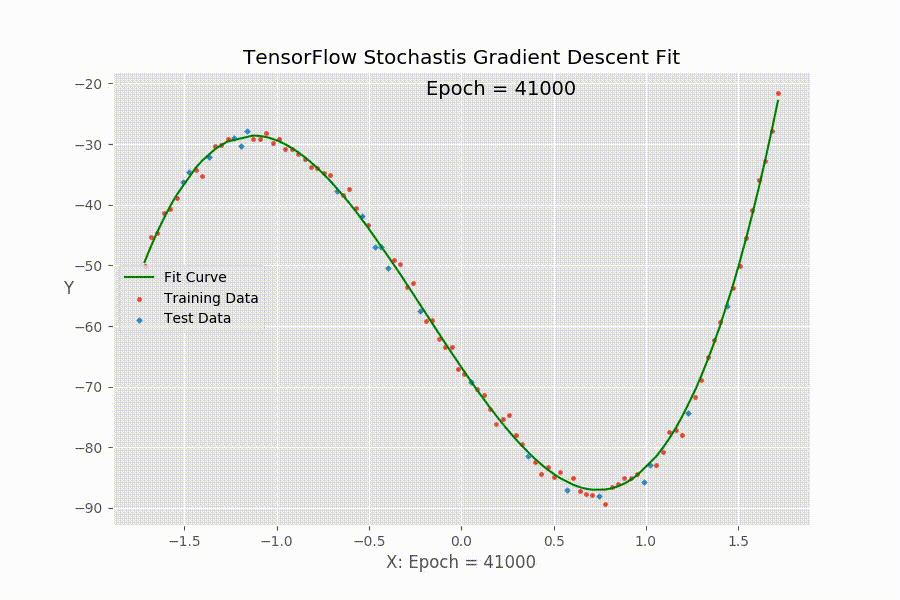
在使用tf的时候,我们需要定义下面几个东西:
1. 输入和输出数据
2. 定义参数
3. 定义损失函数,以及使用什么办法来优化(比如下面使用随机梯度下降的办法)
首先我们需要调用将要使用的一些packages:
import math,sys,os,numpy as np, pandas as pd, tensorflow as tf
from matplotlib import pyplot as plt, rcParams, animation, rc, style
from __future__ import print_function, division
from ipywidgets import interact, interactive, fixed
from ipywidgets.widgets import *
%precision 4
np.set_printoptions(precision=4, linewidth=100)
style.use('ggplot')
%matplotlib inline
plt.rcParams['figure.figsize'] = (12, 9)
rc('animation', html='html5')
我们的目的是使用tf来进行多元回归(这个例子是多项式)。首先我们需要模拟产生一个样本数据:\(X\)是0到9上的均匀分布的点,\(Y\)是\(X\)的多项式函数, \(y = -50 + 30 \cdot x - 12 \cdot x^2 + x^3 + \epsilon\). \(X\)和\(Y\)的关系见下图。
np.random.seed(99)
x = np.linspace(0, 9, 100)[:, np.newaxis]
y = np.polyval([1, -12, 30, -50], x) + np.random.randn(100, 1)
plt.plot(x, y)
plt.xlabel('X')
h = plt.ylabel('Y')
h.set_rotation(0)
plt.title("$y=x^3 - 12 x^2 + 30 x - 50 + \epsilon$")
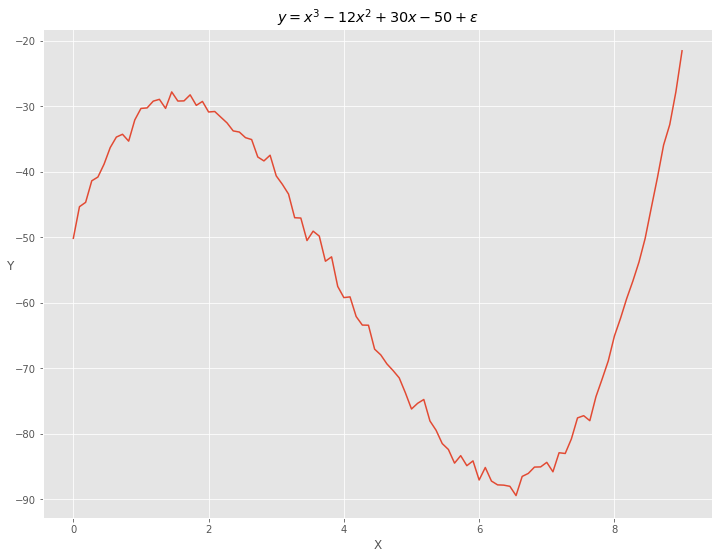
做多项式回归的时候选择基函数为\([1, \space x, \space x^2, \space x^3 ]\),python中可以使用np.power(x, range(4))得到。因为随机梯度下降的时候梯度跟\(X\)的值有关系,所以我们需要对\(X\)的每一列进行标准化让所有的\(X\)的值处在同样的尺度下。
数据标准化的一个办法是所有的值(我们的例子中是每一列数据)减去均值,除以方差
numpy对应的code是(x - x.mean(axis = 0)) / x.std(axis = 0).
另一个办法是每一列数据除以最大值。因为我们的\(X\)都大于0,所以这样做的结果就是把所有的\(X\)变换到\([0, 1]\)区间上。numpy对应的code是x / np.max(x, axis = 0).
pol_order = 4
x = np.power(x, range(pol_order))
def normalized_(x):
return (x - x.mean(axis = 0)) / x.std(axis = 0)
def normalized(x):
l = len(x)
return np.concatenate((np.ones(l).reshape(l, 1), normalized_(x[:, 1:])), axis = 1)
x = normalized(x)
normalized过的\(X\)和\(Y\)的关系为
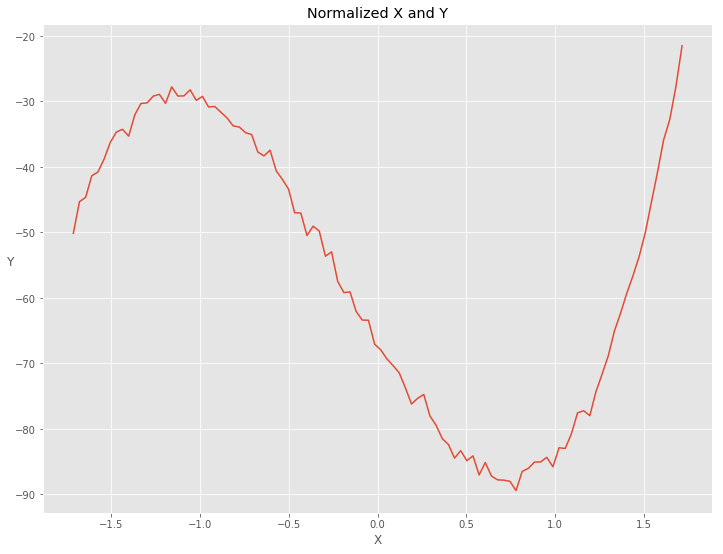
把上面定义好的data分为training和test两部分:
np.random.seed(99)
order = np.random.permutation(len(x))
portion = 20
test_x = x[order[:portion]]
test_y = y[order[:portion]]
train_x = x[order[portion:]]
train_y = y[order[portion:]]
下面开始定义模型。tf通过数据流程图来定义模型,然后编译执行。
我们从定义输入(实际值)输出开始。如前所述,这是通过占位符(placehold)来定义.placehold有两个必须的参数,第一个是数据类型,通常为浮点类型(float).第二个是输入输出的数据的维度。假如我们的输入X是一个(m, n)维的矩阵,我们可以把第二个参数定义为[m, n]。我们用[None n]来表示待定的维度,这样我们可以使用batch来部分的输入数据,而不是全部m个数据。这样做的原因是如果m很大,机器的内存可能处理不了。这时候把数据分为很多batch,每次输入部分的数据(一个batch)来拟合,保证内存不会溢出。我们还可以添加第三个参数name,用来在TensorBoard中展示名字。
with tf.name_scope("Input/Output"):
inputs = tf.placeholder(tf.float32, [None, pol_order], name="X")
outputs = tf.placeholder(tf.float32, [None, 1], name="Yhat")
接下来定义模型表达式。模型的参数变量通过tf.Variable来定义,跟tf.placehold的定义很相似,不同的地方在于tf.Variable的值会随着拟合而发生变化。线性模型的表达式为\(Y=X \times W\)。所以参数W的维度与X的列数相等。矩阵X和W相乘由tf.matmul定义。
with tf.name_scope("Model"):
W = tf.Variable(tf.zeros([pol_order, 1], dtype=tf.float32), name="W")
y = tf.matmul(inputs, W)
最后定义损失函数和它的最优化函数。通常对线性回归模型我们都是要最小化均方误差。损失函数定义为平方损失\(L = \sum_{i=1}^{n}(y_i - f(x_{i}|W)) ^2\)。 把回归函数写成矩阵的形式为\(Y = X \cdot W\),那么损失函数也可以表达为矩阵相乘\(L = (Y - XW)'(Y-XW)\). 要最小化损失函数,我们首先求解出梯度为
tf(包括sklearn)都是通过数值办法来最小化损失函数的,而不是通过解析解,尽管我们知道对线性模型回归参数\(W\)参在解析解\(\hat{W} = (X'X)^{-1}X'Y\). 具体就是让W每次沿着它的梯度方向变化一点点(learning rate),然后反复迭代,直到达到我们的收敛条件或者停止条件。在第一篇中我们介绍过梯度下降的原理:假如损失函数是一座山,我们现在站在山坡上朝四周看看,然后找一个方向能让我们走一点点路但是下降的最快,那个方向就是梯度的方向。
tf提供了很多最优化(不同的梯度下降)的办法,参见Optimizers.对某些数据使用梯度下降的时候会出现鞍点,导致GradientDescentOptimizer可能会找不到最优点或者只是local的最优点。这时应该尝试别的最优化的办法。在我们的例子中,GradientDescentOptimizer找不到最优解, 但是AdamOptimizer可以找到最优解。
learning rate的参数设置为trainable=False表示每次迭代的时候learning rate本身不变化。learning rate太小会导致迭代步骤太多,计算所需要的时间就会很长。learning rate太大也会有问题:在你将要靠近最优点的时候,因为下一步跨的太大,导致跨过了最优点(overshoot)。比较好的办法是:刚开始迭代的时候learning rate可以大一些,然后随着渐渐靠近最优点,learning rate应该渐渐减小。
with tf.name_scope("SGD"):
learning_rate = tf.Variable(0.5, trainable=False)
cost_op = tf.reduce_mean(tf.pow(y-outputs, 2))
train_op = tf.train.AdamOptimizer(learning_rate).minimize(cost_op)
到此为止我们已经准备好了计算流程图,下面我们开始定义对话(session)来执行数据流程图。数据流程图中的每个节点(operation or op)在计算过程当中会获得tensor,每个tensor是一个多为数组。对话将图的op分到cpu或者gpu进行计算。计算完后以tensor返回,在python中其类型为np.ndarray。
1. `sess.as_default()`定义了默认对话, `sess.run()` 和 `sess.eval()` 只能在这个对话下面执行
2. `sess.run()`如果执行`operation`的话(比如`cost_op`),需要提供输入值`feed_dict={inputs: train_x, outputs: train_y}`
3. 对tensor来说,`tensor.eval()` == `sess.run(tensor)`
tolerance = 1e-5
epochs = 1
last_cost = 0
alpha = 0.3
max_epochs = 50000
sess = tf.Session() # default session
# make default session, run() and eval() should be executed in this session
with sess.as_default():
init = tf.initialize_all_variables()
sess.run(init)
sess.run(tf.assign(learning_rate, alpha))
while True:
sess.run(train_op, feed_dict={inputs: train_x, outputs: train_y})
if epochs%100==0:
cost = sess.run(cost_op, feed_dict={inputs: train_x, outputs: train_y})
print ("Epoch: %d - Error: %.4f" %(epochs, cost))
if abs(last_cost - cost) < tolerance or epochs > max_epochs:
print ("Stop Criteria Reached. Break!")
break
last_cost = cost
epochs += 1
w = W.eval() # fetch the value of tensor
print ("w =", w)
print ("Test Cost =", sess.run(cost_op, feed_dict={inputs: test_x, outputs: test_y}))
Epoch: 100 - Error: 1110.4116
Epoch: 200 - Error: 321.6223
Epoch: 300 - Error: 167.4508
Epoch: 400 - Error: 144.2539
Epoch: 500 - Error: 135.3392
Epoch: 600 - Error: 126.8727
Epoch: 700 - Error: 118.1265
Epoch: 800 - Error: 109.2254
Epoch: 900 - Error: 100.3067
Epoch: 1000 - Error: 91.4902
Epoch: 1100 - Error: 82.8799
Epoch: 1200 - Error: 74.5638
Epoch: 1300 - Error: 66.6154
Epoch: 1400 - Error: 59.0937
Epoch: 1500 - Error: 52.0441
Epoch: 1600 - Error: 45.4990
Epoch: 1700 - Error: 39.4793
Epoch: 1800 - Error: 33.9944
Epoch: 1900 - Error: 29.0440
Epoch: 2000 - Error: 24.6189
Epoch: 2100 - Error: 20.7023
Epoch: 2200 - Error: 17.2708
Epoch: 2300 - Error: 14.2958
Epoch: 2400 - Error: 11.7446
Epoch: 2500 - Error: 9.5815
Epoch: 2600 - Error: 7.7693
Epoch: 2700 - Error: 6.2698
Epoch: 2800 - Error: 5.0450
Epoch: 2900 - Error: 4.0584
Epoch: 3000 - Error: 3.2750
Epoch: 3100 - Error: 2.6623
Epoch: 3200 - Error: 2.1907
Epoch: 3300 - Error: 1.8338
Epoch: 3400 - Error: 1.5684
Epoch: 3500 - Error: 1.3748
Epoch: 3600 - Error: 1.2362
Epoch: 3700 - Error: 1.1391
Epoch: 3800 - Error: 1.0725
Epoch: 3900 - Error: 1.0279
Epoch: 4000 - Error: 0.9986
Epoch: 4100 - Error: 0.9800
Epoch: 4200 - Error: 0.9685
Epoch: 4300 - Error: 0.9615
Epoch: 4400 - Error: 0.9574
Epoch: 4500 - Error: 0.9551
Epoch: 4600 - Error: 0.9538
Epoch: 4700 - Error: 0.9531
Epoch: 4800 - Error: 0.9528
Epoch: 4900 - Error: 0.9526
Epoch: 5000 - Error: 0.9525
Epoch: 5100 - Error: 0.9525
Epoch: 5200 - Error: 0.9525
Epoch: 5300 - Error: 0.9525
Stop Criteria Reached. Break!
w = [[ -56.3677]
[ 78.7995]
[-293.1844]
[ 209.9559]]
Test Cost = 1.12171
最终,损失函数在training上面收敛到0.9525,循环达到了停止的条件。这时候损失函数在test上的值为1.12177
最后的拟合函数为
用于拟合的数据的前5行为
| y | x_0 | x_1 | x_2 | x_3 | |
|---|---|---|---|---|---|
| 0 | -32.780156 | 1.0 | 1.645531 | 2.074123 | 2.392560 |
| 1 | -40.784224 | 1.0 | -1.576245 | -1.106391 | -0.877834 |
| 2 | -59.082880 | 1.0 | -0.155892 | -0.426134 | -0.551511 |
| 3 | -73.715893 | 1.0 | 0.155892 | -0.124437 | -0.313780 |
| 4 | -32.524330 | 1.0 | -0.848747 | -0.900180 | -0.822070 |
拟合函数的图像为
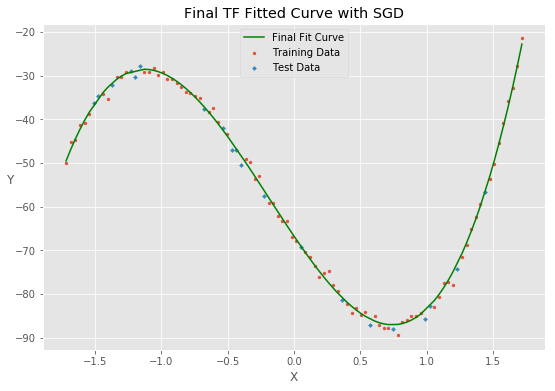

最后说明的是,我们用多元线性回归的例子来演示怎么使用tf. 对于这个问题,python的机器学习package sklearn 可以提供更快捷的结果。
from sklearn import linear_model
from sklearn.metrics import mean_squared_error
reg = linear_model.LinearRegression()
reg.fit(train_x, train_y)
print ("The regression coefficient is %s" %(reg.coef_))
print ("The MSE from sklearn is: %s" %(mean_squared_error(test_y, reg.predict(test_x))))
The regression coefficient is [[ 0. 78.8177 -293.2297 209.9838]]
The MSE from sklearn is: 1.12222708205