快速回顾
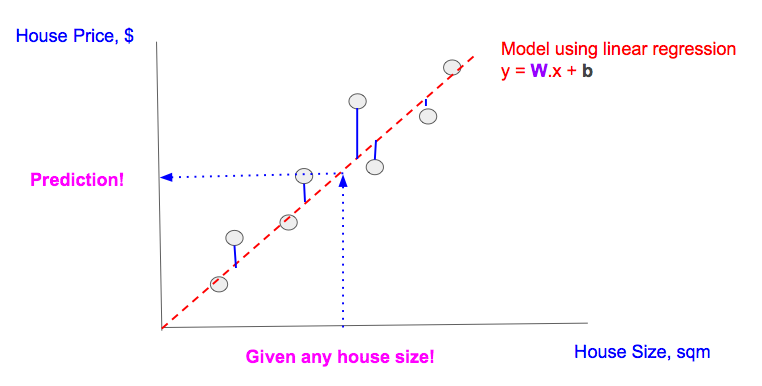
前面两章的前提是:给定房屋面积作为feature,我们想预测房屋价格:
-
我们找到一条直线(线性回归)来最好的拟合数据点。最好的线性回归拟合的意思是:真实值(灰色点)和预测值(灰色点在回归直线上的插值)的距离最小化。也就是那些蓝色线的值最小化。
-
用这条回归直线,对给定的房屋面积,我们可以预测对应的价格
多特征(multi-feature)线性回归回顾
实际当中,预测通常依赖于多个特征。所以我们要从单特征模型拓展到多特征模型。不失一般性,我们选择两个特征模型来可视化。这样既能保持简单,又可以推广到更多特征的情形。
我们引入一个新的特征,房间的数目(房屋里面房间的数目)。在收集数据的时候,我们需要新的特征房间数目,以及已经存在的特征,房屋面积,还有相应的房屋价格。
图形就是3-维的:
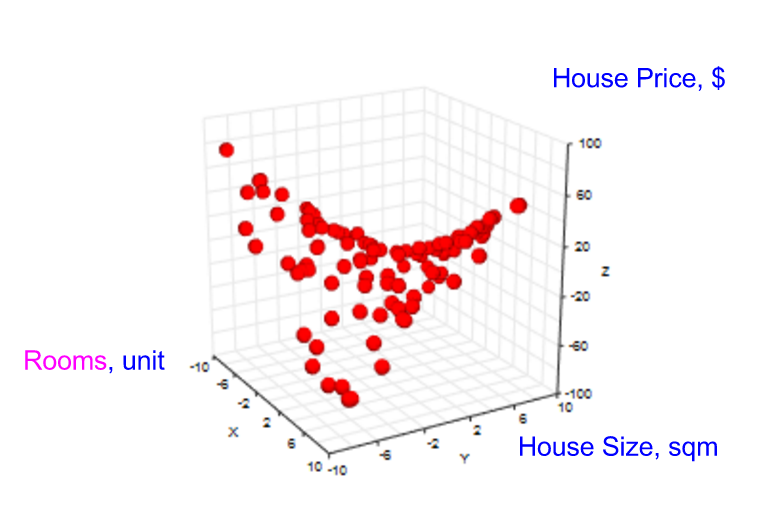
我们的目标是给定房间数目,房屋面积,来预测房屋价格。
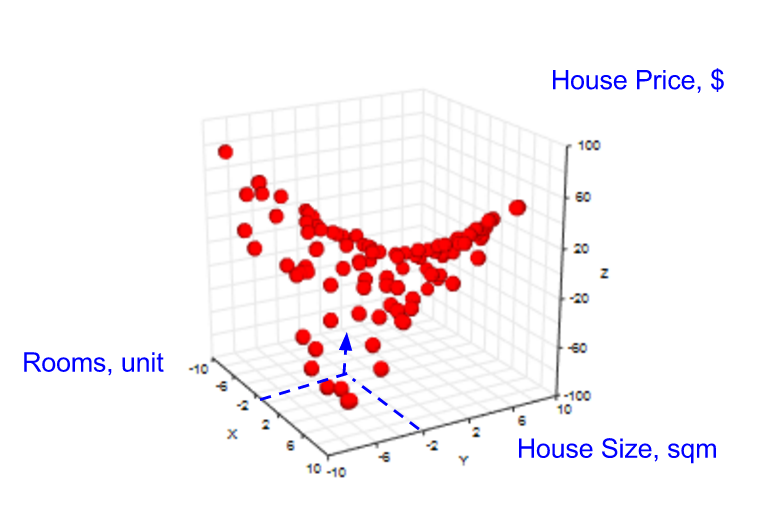
在单特征假设下,我们要用线性回归来产生一条直线来预测房屋面积的结果。在2-维的情形下,我们同样可以做线性回归,只不过变成一个平面(而不是一条直线)。
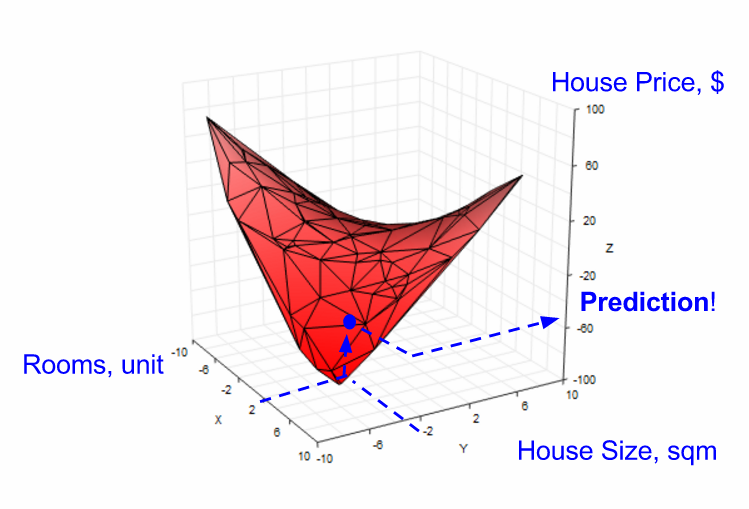
多特征线性回归模型
回忆一下单特征模型(下图左图),线性模型的结果(y)有一个系数(W),一个叫房屋面积的特征的placeholder(x),以及截距b。
对一个2个特征的模型(下图右图),我们有一个新的系数(W2),以及另外一个placeholder叫x2,用来表示房间的数量这个特征。

当我们进行线性回归的时候,梯度下降帮助我们知道W2的值。
TF实现多特征线性回归模型
快速回顾
单特征的TF代码包含三个部分(见下图):
- 建立模型(蓝色部分)
- 构建基于模型的损失函数(红色部分)
- 用梯度下降来最小化损失函数(绿色部分)

TF求解两个特征的线性模型
上面解释的两个特征的线性模型的TF代码表示成红色的颜色:

请注意用这种办法来添加新的feature比较低效。随着特征的数量的增长,变量的数量(W)和placeholder的数量也相应的增长。现实当中的模型会有很多features,导致问题更加严重。我们怎么才能更高效的表示特征?
使用矩阵来表示
首先,我们推广一下从两个feature到n个feature的表示:

用矩阵可以简化n个feature的表达式,TF内嵌了矩阵:
- 数据可以表达成多维,这正好是我们需要的:把一个数据点用n个feature(下图左)和一个有n个系数(下图右,系数矩阵)的模型表达出来。

TF中,它们可以写为
x = tf.placeholder(tf.float, [1,n])
W = tf.Variable(tf.zeros[n,1])
注意,我们用tf.zeros来表示W,也就是说把W=(W1, W2, ..., Wn)全部初始化为0.
- 数学上矩阵相乘是对应的向量点的乘积的和。所以自然的,特征(下图中间)和系数(下图右边)的矩阵相乘就是我们想要的结果(下图左边)。这也就是上面描述的n个特征的线性回归表达式的第一部分(缺少了截距).

TF当中,这个相乘可以表示为
y = tf.matmul(x, W)
- 一个多行的feature矩阵(每一行表示一个数据点的n个feature)乘以系数矩阵就得到多行的结果(每行表示一个数据点的结果)。所以通过矩阵相乘我们可以把线性回归模型表达成数据点的矩阵乘以系数矩阵。
注意: feature矩阵的x的表达式会更加复杂,比如我们用x11,x12而不是x1 x2,这是因为feature矩阵(下图中间)已经从一个数据点的n个feature(1行乘以n列)的变成了m个数据点的n个feature(m行乘以n列)。

TF中的表达形式为
x = tf.placeholder(tf.float, [m, n])
W = tf.Variable(tf.zeros[n,1])
y = tf.matmul(x, W)
- 最后,在矩阵的每一行加一个常数项,就会在结果矩阵中加入常数项
在TF中,x和W已经表达成矩阵,不管有多少个feature或者多少个数据点,都可以简化为
b = tf.Variable(tf.zeros[1])
y = tf.matmul(x, W) + b
Tensorflow多特征备忘录
我们做了一个比较的表格来总结从单feature到多feature的线性回归模型的变化

总结
我们演示了多feature线性回归的概念,以及从单feature到多feature的TF代码。最后用一个速查表做了总结来展示怎么在TF中做多feature回归。
下一步
下一章会讨论logtistic回归,交叉熵(cross-entropy),softmax,这样我们就能更好的明白Tensorflow关于MNIST的官方初级教程。