Logistic Regression回顾

我们已经学习了给定一些features，比如房屋面积，怎么通过TF的线性回归来预测数值型的结果，比如说房屋价格。

但是有时候我们需要进行分类，而不是预测一个数值。比如：给定一些数字的图片，我们希望能识别出0，1，...9.或者给了一首歌，我们希望能识别这是摇滚音乐，乡村音乐或者其他。这种分类的模型识别的结果我们叫class.我们可以用TF中的logistic regression来做分类。

下面我们会讨论用logistic regression来做数字图形识别，也就是分类成0，1，...9.

logistic regression详细介绍

好消息是我们在前面线性回归提到的好多概念在logistic regression继续适用。我们可以使用改进的y=W.x + b。 下面我们看看这两个回归的详细比较

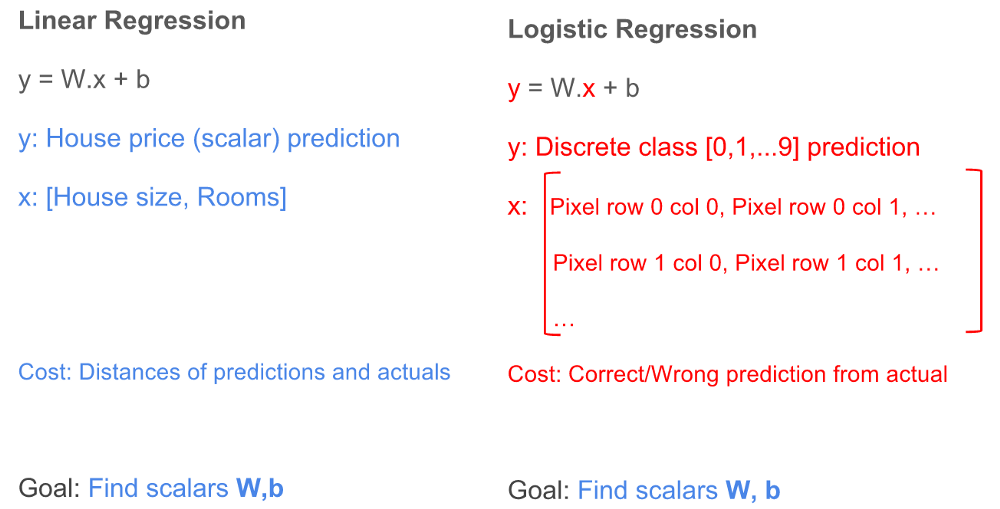
不一样的地方

• 输出的结果(y)：线性回归里面这是一个标量值，比如$50K。在logistic regression里面，这是一个关于类的整数，比如0， 1， 2等等。
• features(x)： 线性回归里面每个feature对应列向量的一个元素。在logistic regression的2-维图像里面，这是一个2维的向量，向量的每个元素表示图片的一个像素。每个像素有一个0-255之间的值，表示对应的灰度：0表示黑色，255表示白色。旁边的值表示不同的灰度。
• 损失函数(cost):线性回归里面我们用的真实值和预测值的平方和。logistic regression里面将会是一个预测正确或者错误的函数。

相似的地方

• training：两个回归的目的都是找出权重(W)和截距(b， biases)的值
• 输出结果:两个回归的结果都是用找出的W和b来预测结果(y)

协调logistic和linear regression

要让y = W.B + x在ligistic regression也工作，我们需要做一些变换来协调上面提到的不同。

Feature (x)的变换

我们可以把logistic regression里的二维的图片的features通过这个办法转化为一维的：把图片的像素矩阵的每一行都粘接到第一行的后面。如下图所示

（译注：实际这儿指的是矩阵变成一个行向量，numpy中如果x是一个矩阵，x.flatten（）就得到我们要的结果）

y的变换

logistic regression中我们不能把y当成标量，因为标量的预测是连续整数，而我们的结果的类是[0, 1, 2， ...]

要克服这一点，y会被变换为一个列向量（下图为了节省地方，表示成行向量），列向量的每个元素表示logistic regression模型认为结果是那个给定的类的得分。在下面的例子中，预测的结果是类1，因为1的得分最高，为33.

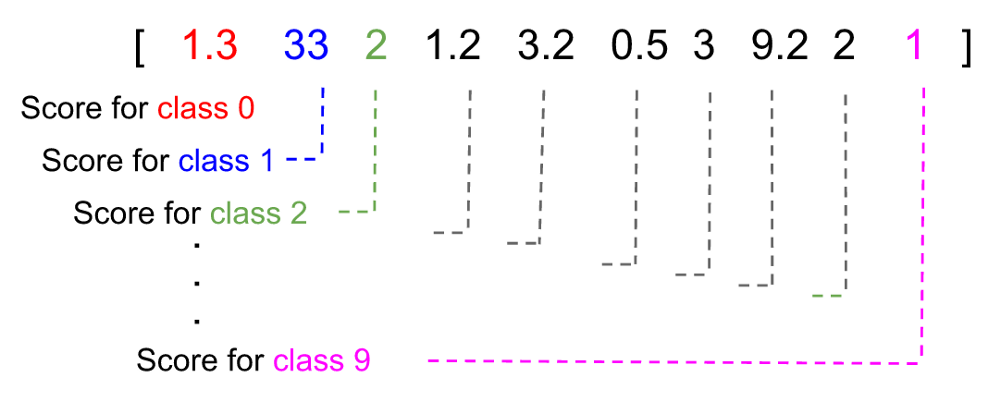
对给定的图片，要得到得分向量，图片的每一个像素，根据它的灰度值，都会被算出一系列的得分（对每个类)用来表示这个像素认为图片被分类到某个类的可能性。对每个类，每个像素的得分的和就是预测向量。

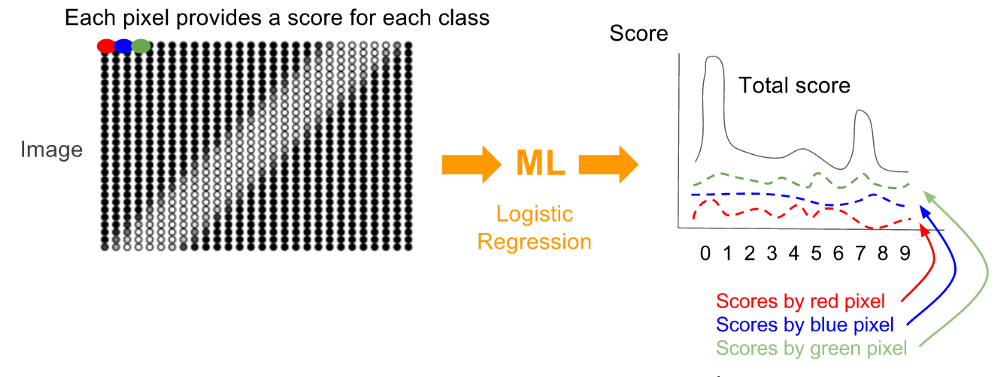
损失函数的变换

因为结果不是数值型的值，我们不能用衡量预测值和真实值的距离的那种数值型的损失函数。这种损失函数，对图像‘1’，会认为预测结果为‘7’（7-1=6）比预测结果为‘2’（2-1=1）更错的严重，尽管实际上两个都是错的。

我们要用的损失函数cross entropy(H)包含下面几步：

1. 把真实的图像的类（y‘）转换为一个one-hot向量，这个向量是一个概率分布

2. 把预测向量（y）转换为一个概率分布

3. 用cross entropy函数来算出损失，这个损失是两个概率分布的距离

stwp 1. one-hot向量

因为我们已经把预测值（y）转换为得分向量了，我们需要把真实值（y）也转换为向量。列向量的每一个元素都是0，只有一个元素是1，这个元素就是真实的类所在的那个位置。这就是one-hot向量，下面是0-9的one-hot向量

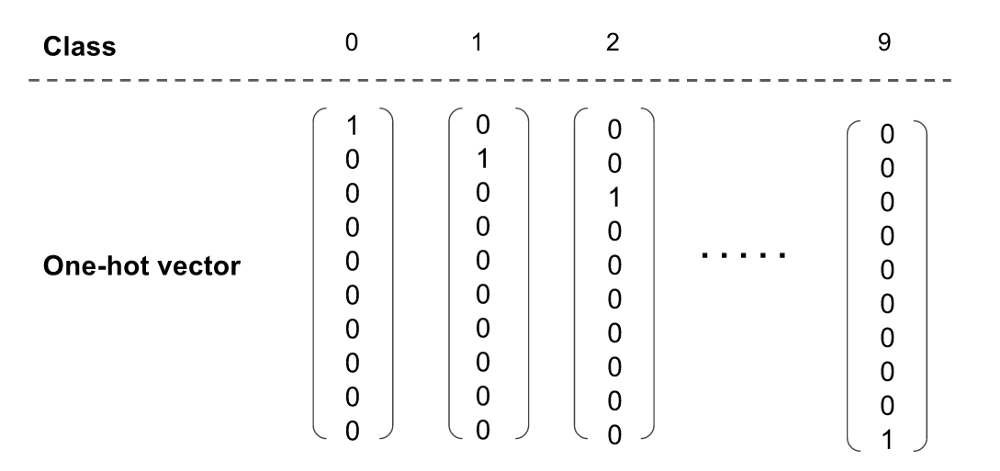
（译注：其实就是产生了一个dummy向量，sklearn的两个变换，其中一个就是one-hot变换）

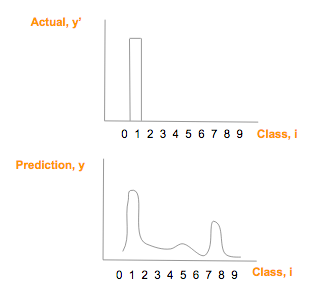
假设真实的（y’）图片为1，那么one-hot向量就是[0, 1, 0, 0, 0, 0, 0, 0, 0, 0], 预测向量 (y) 为 [1.3, 33, 2, 1.2, 3.2, 0.5, 3, 9.2, 1], 把它们画出来比较一下：

step 2. 概率分布和softmax

要数学化的比较两个图片的相似度，cross entropy是一个很好的比较尺度。（这儿有一个很好的详细的例子）

要使用cross entropy，我们需要把真实结果向量（y'）和预测结果向量(y)都转换为概率分布。这儿的概率分布指

• 每个类的概率值在0和1之间
• 对所有类的概率和为1

真实结果向量（y'）是one-hot向量，已经满足这两个条件。

对预测值（y），我们可以用softmax把它转换为概率分布

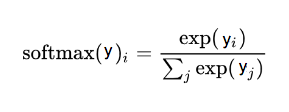
这是一个简单的两步过程（下面S1 和 S2），预测向量（y）的每个值先取指数值，然后除以指数值的总和。

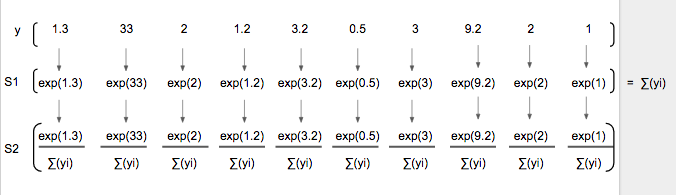
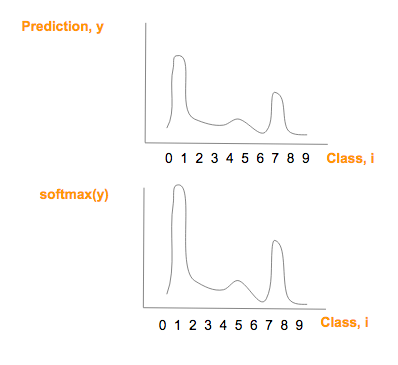
注意softmax（y）的图像跟预测值（y）的图像很相似，只是最大值更大，最小值更小

setp 3. cross entropy

我们现在可以来计算预测向量（y）的概率分布和真实向量（y'）的cross entropy(H) 了。

cross entropy的公式为

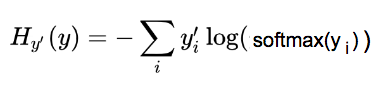
要快速理解这个复杂的公式，我们把它分为三部分。注意下面的公式H中，我们用y_i来表示‘y向量的第i个元素’

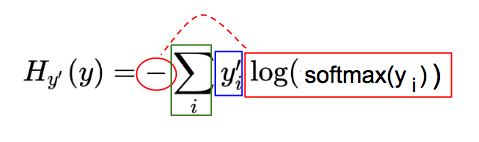
• 蓝色： 真实结果向量，y_i'
• 红色： 预测向量的概率分布(softmax(y_i))的log值
• 绿色： 对每个图像的分类i，i=0到9，上面红色和蓝色的乘积的和

下面的例子可以用来帮助理解。

蓝色的部分是ont-hot真实结果(y')向量

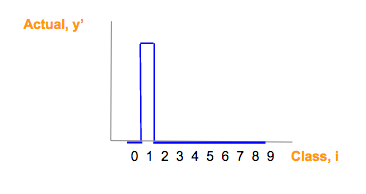
红色部分是从预测向量y的推导得到，也就是从softmax(y)到-log(softmax(y))

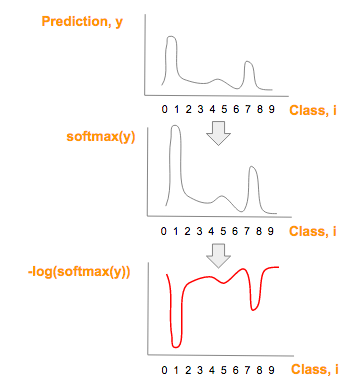
如果你想进一步了解为什么用-log(softmax(y))来代替softmax(y)，请看这个视频 或者文件

cross entropy(H)，下图中的绿色部分，是蓝色和红色部分的乘积，然后把它们加起来

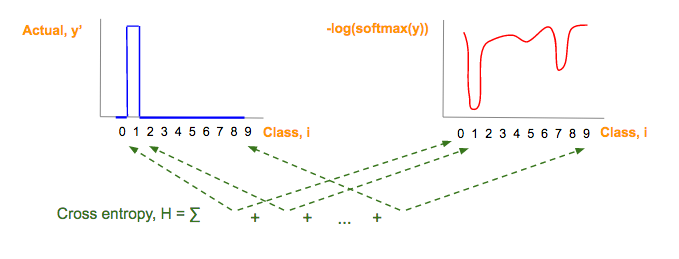
因为蓝色部分是one-hot向量，只有一个对应真实分类的元素是1，别的元素都是0.所以H可以简化为

Cross Entropy (H) = -log(softmax(y_i))
Where:
- y_i: Predicted score/probability for correct image class

归纳

根据上面的三个变换，我们可以使用线性模型的技术来做logistic regression。下面的代码逐行比较了线性模型部分和logistic regression部分的区别

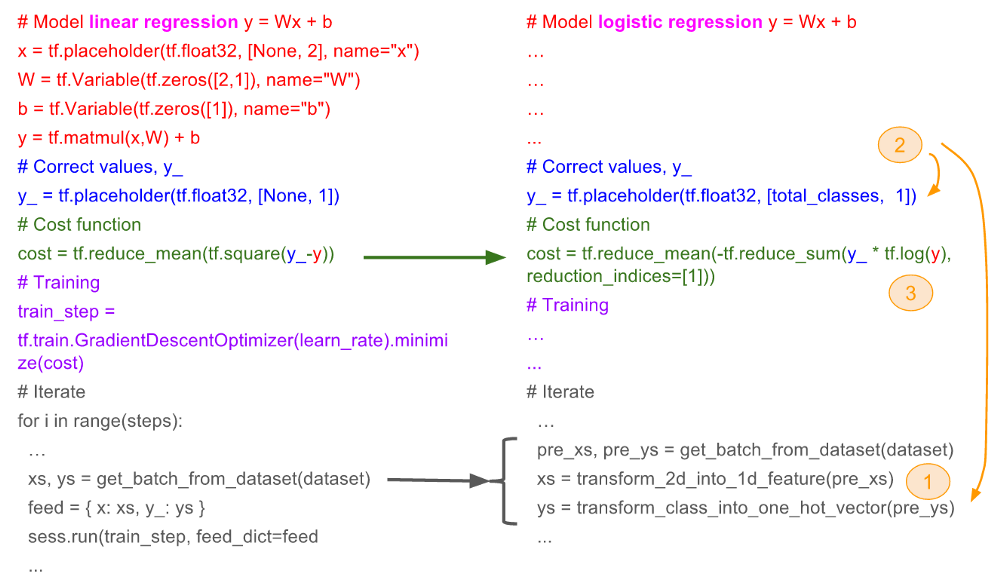
1. Feature(x)变为一维的feature

2. 预测向量(y_)和真实向量(y)变为one-hot向量

3. 损失函数从均方误差损失变为cross entropy

下面是不同的地方的总结

总结

给定几个feature的时候，线性模型可以用来预测数值型的结果。logistic regression可以用来分类。

我们用例子演示了怎么通过三个改变，从线性回归y = W.x + b做logistic regression。三个改变为: (1) feature向量 (2)预测值/真实结果向量 (3)损失函数

通过上面介绍的one-hot向量，softmax，已经cross entropy，下面你可以很轻松的阅读google官方的关于图片分类的简易教程了.

Reference

1. Gentlest Intro to Tensorflow #4: Logistic Regression