Intro
通常介绍deep learning的时候总是从卷积神经网络开始,因为最近deep learning的流行就是从卷积神经网络在图像识别上的广泛应用开始的。但是在银行这种地方,没有什么明显的图像处理的需求。更多的是要处理各种序列性的数据,比如时间序列等等。所以这里我会从循环神经网络(RNN)开始,并且结合一个例子用来展示怎么进行时间序列的建模。
RNN的一个显著特征是:新的输入(下图t时刻的输入,绿色的箭头)会和前一个state(下图从t-1到t的蓝色箭头)一起变成新的输入。并以此循环。
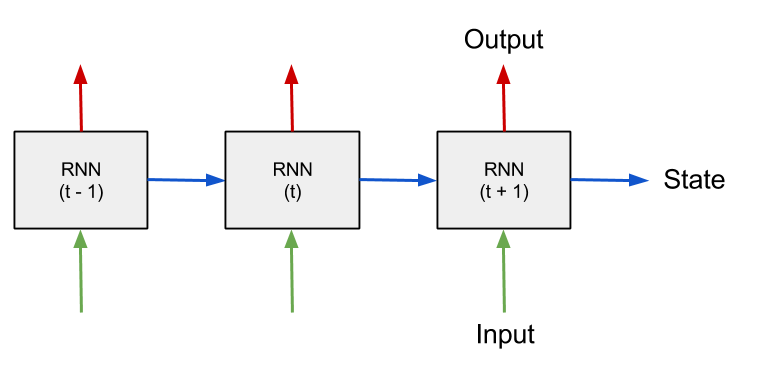
把上图画成下图的等号右边部分,那么整个的循环过程通常也就画为下图的等号左边部分。
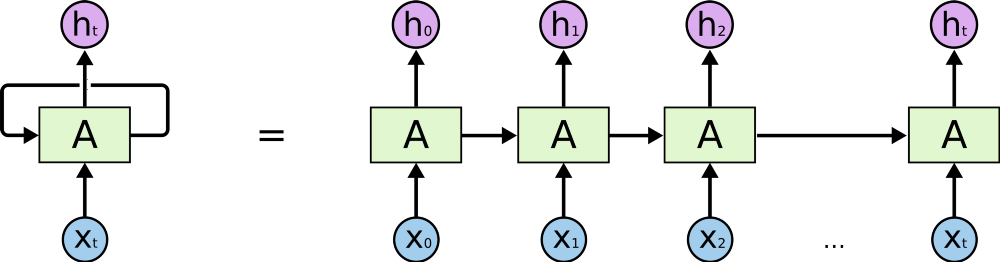
RNN好的地方是它可以记住前面一段时间的输入信息,不好的地方是它只能记住某段时间的输入信息,虽然理论上RNN可以处理长时间的信息,但是实际上它却不能很好的学习这些信息。对于长时间的输入信息它无能为力。
对RNN的一个改进就是长短记忆网络(LSTM). LSTM通过信息阀门来控制信息是否能够通过。这个信息阀门是由一个sigmoid神经网络层和多元运算符组成。sigmoid网络层的输出是一个0,1之间的值,用来控制每个组成部分有多少信息可以通过。0表示没有信息能够通过,1表示所有的信息都可以通过。通过控制不同的信息加入到cell state中,LSTM实现了控制哪些信息可以对最后的stage施加影响。
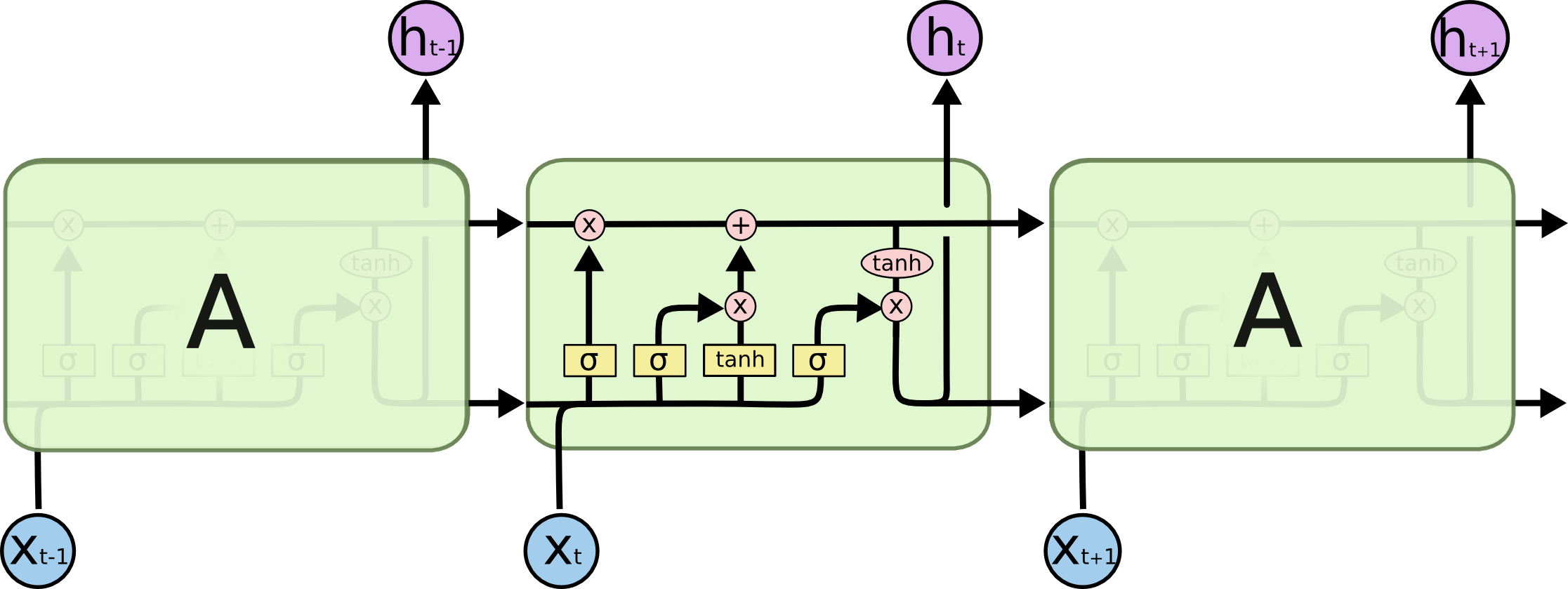
上面图中的各个标志的表示意义分别为

LSTM在自然语言处理(NLP),自动翻译上面取得了很大的成功。如果我们换一个视角,把RNN/LSTM中的输入当成是按照时间顺序的排列的数据,它们就可以用来对(高维)时间序列建模和预测。我们可以控制在RNN/LSTM的每个输入的Layer上输出或者不输出,这样我们就很容易的进行一步预测比如\(X_{1}, X_{2}, \cdots, X_{n-1}\)来预测\(\hat{X_{n}}\),或者进行多步预测,比如用\(X_{1}\)来预测\(\hat{X_{2}}\),\(\hat{X_{2}}\)来预测\(\hat{X_{3}}\)等等。
有一些实际的例子表明,在\(X_{1}, X_{2}, \cdots, X_{n-1}\)来预测\(\hat{X_{t}}\)中,即使不需要\(\hat{X_{2}}, \cdots, \hat{X_{n-1}}\),但是在模型中强制这些输出会提高模型的效果。
也有一些实际的例子显示,经过改进CNN也可以用来处理这种序列性质的数据,而且可以得到比RNN更好的效果。
1. DATA & Model
1.1. 数据来源
使用的数据是S&P500从02Jan1998到09Aug2013攻击3926天每天的股票价格数据,包括OHLCV,共计500只股票。
1.2. 数据转变
对每一只股票,计算出它的每天几种不同价格的比值,比如Open对Close(c_2_o),High(c_2_h)以及Low(c_2_l)的比值,以及High对Close(h_2_c)和Low(h_2_l)的比值。因为各个股票的Volume会很不相同,为了让它们在同一个Scale上面,对Volume进行标准化,即减去均值,除以标准差。这些每只股票每天自身的性质会作为我们的自变量input。我们想做的是用这些来预测股票第二天是上涨还是下跌。也就是t+1时间的Close价格除以t时间的价格(c1_c0)。如果第二天上涨了,那么比值大于1,比值的对数函数就大于0.反之这个Close的价格的比值的对数函数就小于0.所有的数据可以从quantquote下载。
因为不是所有的500只股票都有完整的3926天的数据,只有388只股票有完整的数据。取这388只股票上面所说的6个比值作为最后的X,取这388只股票的回报率的均值作为Y.Y可以理解为在388只股票上每只股票投资一块钱的平均回报率。从3926行数据中去前3900行作为最后的分析数据。所以最后X的维度为(3900, 2328),Y的维度为(3900, 1).
1.3. 数据说明
1.3.1. 理想状况
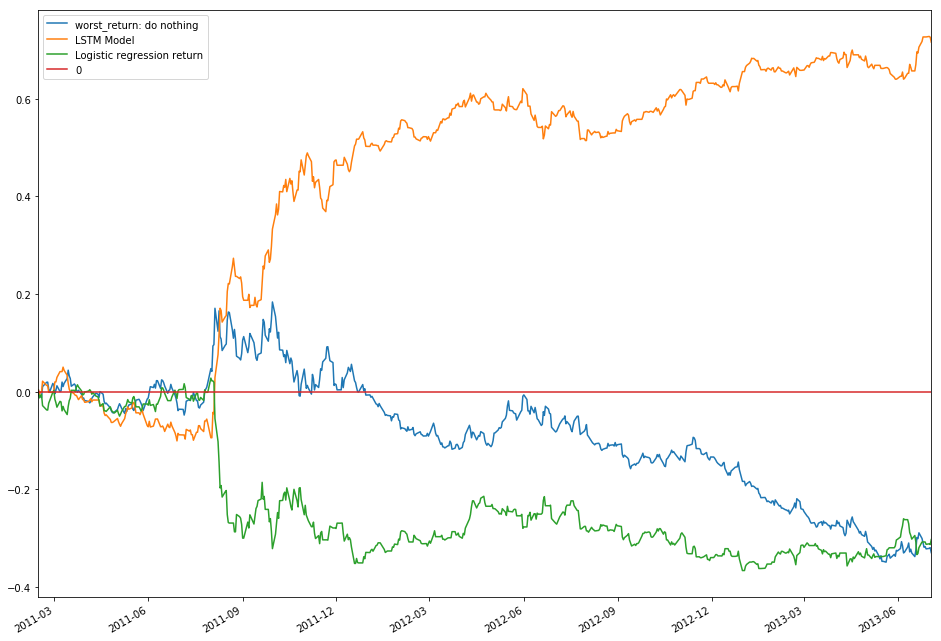
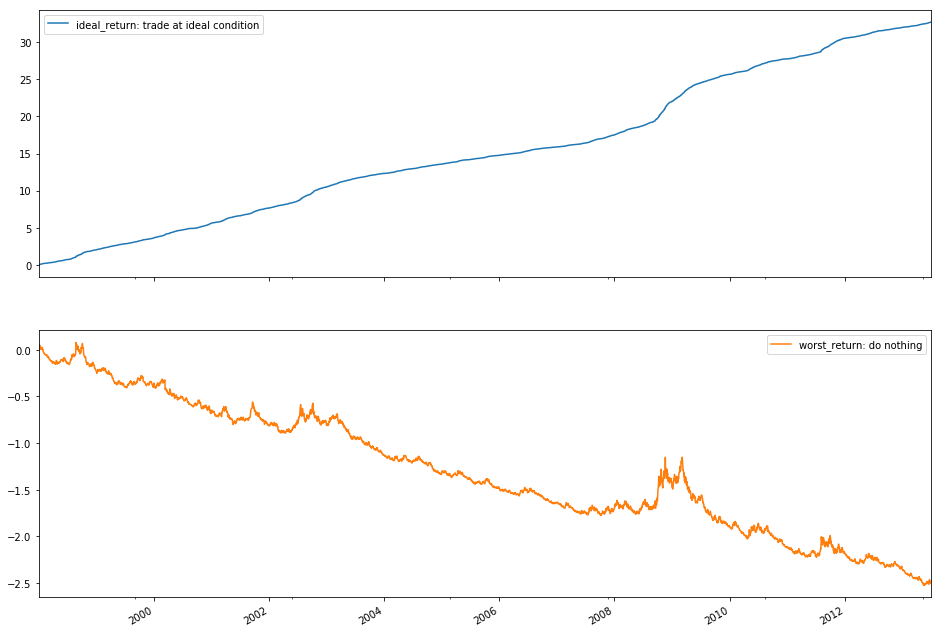
假如我们已经知道Y的值是大于0还是小于0,我们可以做出最优的决定:对任一天,当第二天的价格高于当天的价格的时候,我们买进一块钱然后第二天卖掉,这样我们就可以赚取那一部分差价。如果第二天的价格低于今天的价格,我们就应该在今天卖一块钱的股票。这样的决策成为理想决策。当然实际上因为没法知道第二天的价格,所以这样的决策不存在。但是因为我们是历史数据,我们还是可以计算出理想决策最终可以获得多少利润。
1.3.2. 最差状况
最差的状况就是投一块钱,然后什么都不做最后所得到的状态。
1.4. 学习模型
因为回报率是一个连续值,但是我们实际关系的是它大于0还是小于0.所以我们把它分为11份,记为0到10.这样的话Y就是一个Categorical Variable,问题也就转化为一个有序分类(ordered categorical data)的问题。如果预测的\(\hat{Y} < 5\),我们应该卖出。如果\(\hat{Y} == 5\),则不作任何交易。如果\(\hat{Y} > 5\),则买入。
1.4.1. Multinomial Logistic Regression
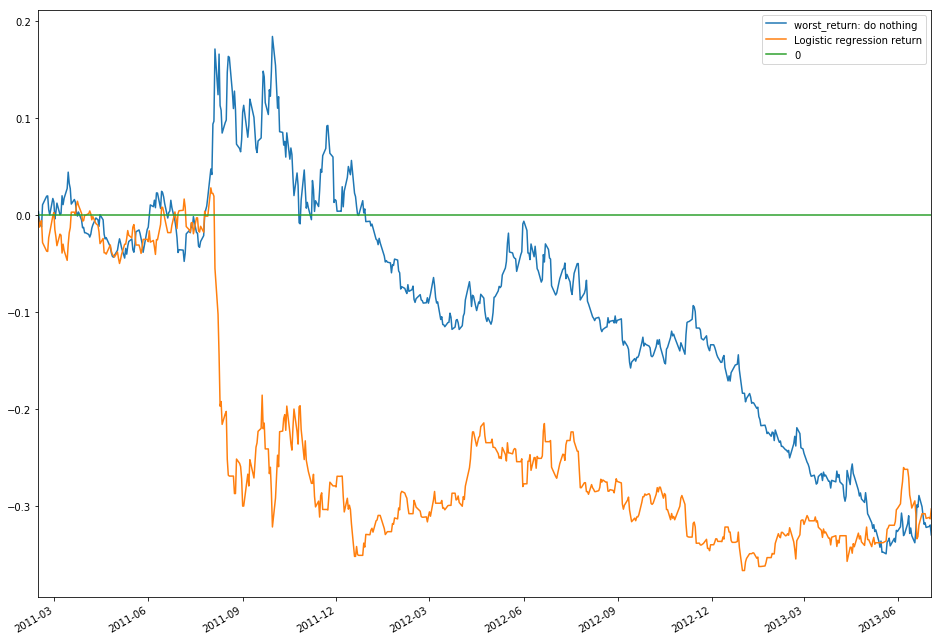
类似于传统的logistic regression,只是这个时候Y不只是0和1,而是0到10.因为只是logistic regression,没有超参数,也没有变量选择,所以效果不是很好。
1.4.2. LSTM Model
LSTM会根据输入的数据来有选择的记住前面的信息。这里我们使用tensorflow的MultiRNNCell([LSTMCell() for _ in range(2)])建立了一个两层的LSTM模型。可以看出,LSTM明天的提高了预测的效果。