Build Recurrent Neural Network from Scratch

0. Introduction

The previous blog shows how to build a neural network manualy from scratch in numpy with matrix/vector multiply and add. Although there are many packages can do this easily and quickly with a few lines of scripts, it is still a good idea to understand the logic behind the packages. This part is from a good blog which use an example predicitng the words in the sentence to explain how to build RNN manually. RNN is a little more complicated than the neural network in the previous blog because the current time status and ourput in RNN will depends on the status in the previous time. So the Backpropagation part will be more complicated. I try to give the details in mathematic formula about how to get the gradients recursively in the partial derivatives.

Recurrent neural network is one of the most popular neural networks for language modeling(based on existed words to predict next word) or automatic input like the automatic complete in the mobile input(based on existed character to predict next character).

For example, when we build a RNN for language, that means: the training data is a list of sentences. Each sentence is a seris of words(tokenized words). For each sentence, from the first word, we will predict the second word. From the first and the second word, we will predict the third word, etc. Recurrent neural network means when it predict time order t, it will remember the information from time order 0 to time order t.

Let's denote the sentence having \(t+1\) words as \(x=[x_0, x_1, \cdots, x_t]\). We start from \(x_0\) to status \(s_0 = \tanh(Ux_0 + Ws_{-1})\), where \(s_{-1}\) is the initialization of status initialized as 0. The output \(o_0 = \mathrm{softmax}(Vs_0)\). Then when we go to next word \(x_1\) we will have updated status \(s_1 = \tanh(Ux_1 + Ws_0)\) and the corresponding output \(o_1 = \mathrm{softmax}(Vs_1)\). You will see at time order \(t=1\) it not only depends on input \(x_1\) but also depends on the previous status \(s_0\). The equation for the RNN used in this tutorial is:

\begin{aligned} s_t &= \tanh(Ux_t + Ws_{t-1}) \\ o_t &= \mathrm{softmax}(Vs_t) \end{aligned}

If we plot the logic of RNN and the corresponding forward propagation, it is like alt text

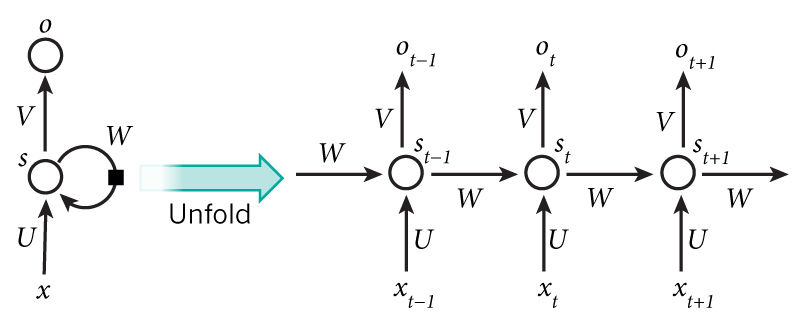
The training data is 79,170 sentences coming from 15,000 reddit comments(one comment may has multiple sentences). The vocabulary consists of the 8,000 most common words. For the words not included in the vocabulary list are replaced by UNKNOWN_TOKEN.

The words in each sentences are mapped to the index of the order of these words in the vocabulary list. So the training data \(X\) and \(Y\) are both integers rather than strings. Since the purpose here is to predict the next word, so \(Y\) is just \(X\) shifted by one leading position.

1. Build RNN

1.0. Model and Data Structure, Initialization

As introduced before, the model structure of RNN used here is:

\begin{aligned} s_t &= \tanh(Ux_t + Ws_{t-1}) \\ o_t &= \mathrm{softmax}(Vs_t) \end{aligned}

The vocabulary size \(C=8,000\) and the hidden layer size \(H=100\). So the size of W is \(100 \times 100\).

Let's assume one sentence has 10 words, for the corresponding mapped \(x\), we can treat it in two equal ways: 1. it is a python list by index of the words in the sentence. Then its length is the same as the number of words in that sentence, which is 10. we call it x_expression_1; 2. it is the one-hot transformation of these 10 words in the 8,000 vocabulary list. so its shape is [10, 8000]. For each row, there is one 1 in the word index position and the other 7999 positions will be all 0. we call it x_expression_2. So for each word of these 10 words, the matrix dot multiply \(U.\)dot\((x\_expression\_2[t])\) is the same as \(U[:, x\_expression\_1[t]]\) for \(t = \mathrm{range(10)}\).

If use numpy to explain above, it is np.arange(1, 21).reshape(4, 5).dot([0,1,0,0,0]) == np.arange(1, 21).reshape(4, 5)[:, 1]. This will save a lot of time because numpy indexing is much faster than matrix dot multiply.

The dimension of all the data used is(below \(x_t\) is index position in the vocabulary list for the \(t_{th}\) word in the sentence, and \(x\) is a sentence with \(l\) words):

\begin{aligned} x_t &\in \mathbb{R}^{8000} \Longleftrightarrow x \in \mathbb{R}^{l \times 8000} \\ o_t &\in \mathbb{R}^{8000} \Longleftrightarrow o \in \mathbb{R}^{l \times 8000} \\ s_t &\in \mathbb{R}^{100} \Longleftrightarrow s \in \mathbb{R}^{l \times 100} \\ U &\in \mathbb{R}^{100 \times 8000} \\ V &\in \mathbb{R}^{8000 \times 100} \\ W &\in \mathbb{R}^{100 \times 100} \\ \end{aligned}

When we iterate to update the parameters, we need to set up their initial values. It is very important to set up suitable initializations to make RNN gradients work well. The initizalition of the parameters is initialized as from random uniform distribution \(U\left(-\frac{1}{\sqrt{n}}, \frac{1}{\sqrt{n}} \right)\) :

import numpy as np
import itertools
import operator
from datetime import datetime
import sys

vocabulary_size = 8000

X_train = np.load('X_train.npy')
y_train = np.load('y_train.npy')

## initialize parameters
class RNNNumpy():
    def __init__(self, word_dim, hidden_dim = 100, bptt_truncate = 4):
        # assign instance variable
        self.word_dim = word_dim
        self.hidden_dim = hidden_dim
        self.bptt_truncate = bptt_truncate
        # random initiate the parameters
        self.U = np.random.uniform(-np.sqrt(1./word_dim), np.sqrt(1./word_dim), (hidden_dim, word_dim))
        self.V = np.random.uniform(-np.sqrt(1./hidden_dim), np.sqrt(1./hidden_dim), (word_dim, hidden_dim))
        self.W = np.random.uniform(-np.sqrt(1./hidden_dim), np.sqrt(1./hidden_dim), (hidden_dim, hidden_dim))

Pay attention: the matrix \(U, V, W\) are not initizalized as matrix with value 0 but random numbers. If you initilize them as 0, then you will get everythin 0 and they will not change in the loop.

1.1. Forward-Propagation

For a given sentence \(x = (x_0, \cdots, x_{T-1})\) having \(T\) words, we will start from \(x_0\) with initialized \(s_{-1} = 0\) to calculate \(s_0\) and \(o_0\), then from \(s_0\) together with \(x_1\) to get \(s_1\) and \(o_1\), and so on.

## 1. forward propagation

def softmax(x):
    xt = np.exp(x - np.max(x))
    return xt / np.sum(xt)

def forward_propagation(self, x):
    # total num of time steps, len of vector x
    T = len(x)
    # during forward propagation, save all hidden stages in s, S_t = U .dot x_t + W .dot s_{t-1}
    # we also need the initial state of s, which is set to 0
    # each time step is saved in one row in s，each row in s is s[t] which corresponding to an rnn internal loop time
    s = np.zeros((T+1, self.hidden_dim))
    s[-1] = np.zeros(self.hidden_dim)
    # output at each time step saved as o, save them for later use
    o = np.zeros((T, self.word_dim))
    for t in np.arange(T):
        # we are indexing U by x[t]. it is the same as multiplying U with a one-hot vector
        s[t] = np.tanh(self.U[:, x[t]] + self.W.dot(s[t-1]))
        o[t] = softmax(self.V.dot(s[t]))
    return [o, s]

RNNNumpy.forward_propagation = forward_propagation

Each \(o_t\) here is a vector of prob representing the word in the vocabulary list. All we want is the next word with the predicted prob, we call it predict

def predict(self, x):
    o, s = self.forward_propagation(x)
    return np.argmax(o, axis = 1)

RNNNumpy.predict = predict

np.random.seed(10)
model = RNNNumpy(vocabulary_size)
o, s = model.forward_propagation(X_train[10])
print(o.shape)
print(o)

predictions = model.predict(X_train[10])
print(predictions.shape)
print(predictions)

(45, 8000)
[[ 0.00012408  0.0001244   0.00012603 ...,  0.00012515  0.00012488
   0.00012508]
 [ 0.00012536  0.00012582  0.00012436 ...,  0.00012482  0.00012456
   0.00012451]
 [ 0.00012387  0.0001252   0.00012474 ...,  0.00012559  0.00012588
   0.00012551]
 ..., 
 [ 0.00012414  0.00012455  0.0001252  ...,  0.00012487  0.00012494
   0.0001263 ]
 [ 0.0001252   0.00012393  0.00012509 ...,  0.00012407  0.00012578
   0.00012502]
 [ 0.00012472  0.0001253   0.00012487 ...,  0.00012463  0.00012536
   0.00012665]]
(45,)
[1284 5221 7653 7430 1013 3562 7366 4860 2212 6601 7299 4556 2481  238 2539
   21 6548  261 1780 2005 1810 5376 4146  477 7051 4832 4991  897 3485   21
 7291 2007 6006  760 4864 2182 6569 2800 2752 6821 4437 7021 7875 6912 3575]

1.2. Lost Function

We will use cross entropy loss function here. If we have \(N\) training examples(words in the text) and \(C\) classes(the size of the vocabulary list), then the lost function with respect to the prediction \(o\) and the true lable \(y\) is:

\begin{aligned} L(y, o) = - \frac{1}{N}\sum_{n \in N}y_n \log o_n \end{aligned}

How do we know this loss function makes sense?

If everything is predicted correctly, that is: for the \(y_i = 1\), the corresponding \(o_i = 1\), then \(1 \times \log(1) = 1 \times 0 = 0\). For the rest \(y_i = 0\), the multiplied value \(0 \times \log(o_i) = 0\). So the loss will be 0 for the perfect function.

On the other way, if the model have no prediction power, then all \(o_i = 1/C\) then we will have \(L(y, o) = - \frac{1}{N}\sum_{n \in N} \log \frac{1}{C} = \log(C)\).

## 2. calculate the loss
'''
the loss is defined as
L(y, o) = -\frac{1}{N} \sum_{n \in N} y_n log(o_n)
'''
def calculate_total_loss(self, x, y):
    L = 0
    # for each sentence ...
    for i in np.arange(len(y)):
        o, s = self.forward_propagation(x[i])
        # we only care about our prediction of the "correct" words
        correct_word_predictions = o[np.arange(len(y[i])), y[i]]
        # add to the loss based on how off we were
        L += -1 * np.sum(np.log(correct_word_predictions))
    return L

def calculate_loss(self, x, y):
    # divide the total loss by the number of training examples
    N = np.sum((len(y_i) for y_i in y))
    return self.calculate_total_loss(x, y)/N

RNNNumpy.calculate_total_loss = calculate_total_loss
RNNNumpy.calculate_loss = calculate_loss

print("Expected Loss for random prediction: %f" % np.log(vocabulary_size))
print("Actual loss: %f" % model.calculate_loss(X_train[:1000], y_train[:1000]))

Expected Loss for random prediction: 8.987197
Actual loss: 8.987440

1.3. Model Training with Backward-Propagation

Next we need to find the value of \(U, V, W\) to minimize the loss function. SGD is the common way to do this. The idad behind SGD is: we iterate over all the training examples and during each iteration we nudge the parameters into a direction that reduces the error. The direction is given by the gradient of th loss \(\frac{\partial{L}}{\partial{U}}, \frac{\partial{L}}{\partial{V}}, \frac{\partial{L}}{\partial{W}}\). SGD also needs learning rate, which defines how big of a step we want to make in each iteration. You can refer to here for SGD introduction. SGD is a common method used in many numeric solutions to optimize the function.

Now the question becomes how to calculate the gradients \(\frac{\partial{L}}{\partial{U}}, \frac{\partial{L}}{\partial{V}}, \frac{\partial{L}}{\partial{W}}\). In the regular fully connected neural network, we use backpropagation to calculate it. In RNN it is a little more complicated because of the hidden status which links the current time step with the historical time step. So we need to calculate the gradients through the time. Thus we call this algorithm backpropagation through time(BPTT). The parameters are shared in all the time steps, the gradients at each output will not only depends on the current time step, but also the previous time steps. For general introduction of backpropagation, please read this and this. Here I will give some detailed math formula about the BPTT used in this post.

Let's look at the graph of RNN below. Suppose now we are at time step \(t=3\), we want to calculate the gradients.

alt text

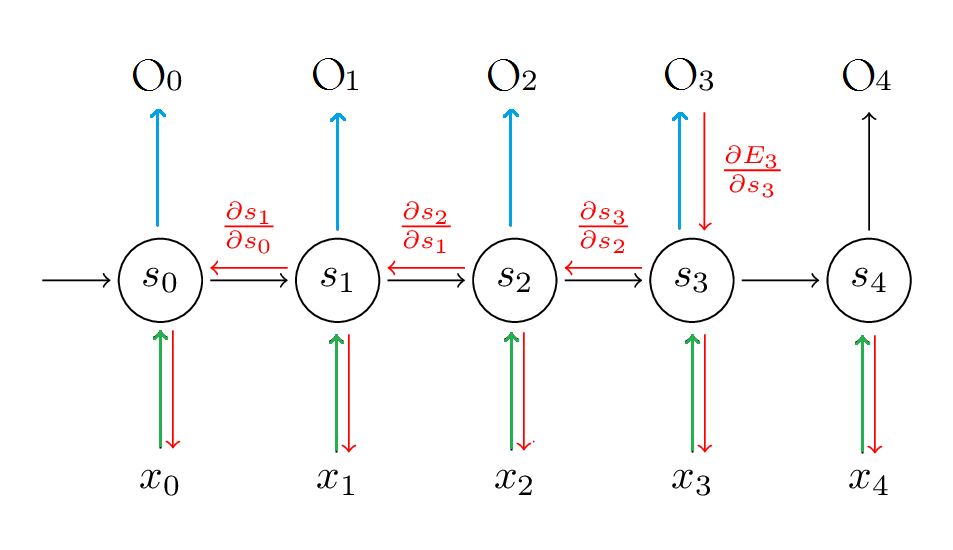
To make it clear, I will write the forward propagation explitly:

\begin{aligned} & s_0 = tanh(U x_0 + W s_{-1}) \\ & z_0 = V s_0 \\ & o_0 \triangleq \hat{y}_{0} = sigmoid(z_0) \\\\ & s_1 = tanh(U x_1 + W s_0) \\ & z_1 = V s_1 \\ & o_1 \triangleq \hat{y}_{1} = sigmoid(z_1) \\\\ & s_2 = tanh(U x_2 + W s_1) \\ & z_2 = V s_2 \\ & o_2 \triangleq \hat{y}_{2} = sigmoid(z_2) \\\\ & s_3 = tanh(U x_3 + W s_2) \\ & z_3 = V s_3 \\ & o_3 \triangleq \hat{y}_{3} = sigmoid(z_3) \\ \end{aligned}

Also, for simplification, I will treat everything as scale rather then vectors or matrix. This will make the partial derivative easy to understand. After we understand this, we only need tiny modification to replace some multiplication by the array dot multiply.

First, let's denote

\begin{aligned} & d_3 \triangleq \big(\hat{y}_3 - y_3 \big) \cdot V \cdot \big(1 - s_3 ^ 2 \big) \\ & d_2 \triangleq d_3 \cdot W \cdot \big(1 - s_2 ^ 2 \big) \\ & d_1 \triangleq d_2 \cdot W \cdot \big(1 - s_1 ^ 2 \big) \\ & d_0 \triangleq d_1 \cdot W \cdot \big(1 - s_0 ^ 2 \big) \\ \end{aligned}

1.3.1. Calculate of partial derivative of error \(E_3\) to \(U\): \(\frac{\partial{L}}{\partial{U}}\)

We have already know each historical hidden status will be used to calculate current status. The parameters are used in each status. So we need to calculate all the hidden status to the parameter \(U\).

\begin{aligned} \frac{\partial{s_0}}{\partial{U}} &= \big(1 - s_0 ^ 2 \big) \left(x_0 + \frac{\partial{s_{-1}}}{\partial{U}} \right) \\ &= \big(1 - s_0 ^ 2 \big) \cdot x_0 \\\\ \frac{\partial{s_1}}{\partial{U}} &= \big(1 - s_1 ^ 2 \big) \left(x_1 + W \cdot \frac{\partial{s_{0}}}{\partial{U}} \right) \\ &= \big(1 - s_1 ^ 2 \big) \big(x_1 + W \cdot \big(1 - s_0 ^ 2 \big) \cdot x_0 \big) \\\\ \frac{\partial{s_2}}{\partial{U}} &= \big(1 - s_2 ^ 2 \big) \left(x_2 + W \cdot \frac{\partial{s_{1}}}{\partial{U}} \right) \\ &= \big(1 - s_2 ^ 2 \big) \Big(x_2 + W \cdot \big(1 - s_1 ^ 2 \big) \big(x_1 + W \cdot \big(1 - s_0 ^ 2 \big) \cdot x_0 \big) \Big)\\\\ \frac{\partial{s_3}}{\partial{U}} &= \big(1 - s_3 ^ 2 \big) \left(x_3 + W \cdot \frac{\partial{s_{2}}}{\partial{U}} \right) \\ &= \big(1 - s_3 ^ 2 \big) \\ & \bigg(x_3 + W \cdot \big(1 - s_2 ^ 2 \big) \Big(x_2 + W \cdot \big(1 - s_1 ^ 2 \big) \big(x_1 + W \cdot \big(1 - s_0 ^ 2 \big) \cdot x_0 \big) \Big) \bigg)\\\\ \end{aligned}

After we get this, we can calculate the partial derivative of error \(E3\) to \(U\):

\begin{aligned} \frac{\partial{E_3}}{\partial{U}} &= \frac{\partial{E_3}}{\partial{\hat{y}_3}} \frac{\partial{\hat{y}_3}}{\partial{z_3}} \frac{\partial{z_3}}{\partial{s_3}} \frac{\partial{s_3}}{\partial{U}} \\ &= \left(\frac{\partial{E_3}}{\partial{\hat{y}_3}} \frac{\partial{\hat{y}_3}}{\partial{z_3}} \right) \cdot \frac{\partial{z_3}}{\partial{s_3}} \cdot \frac{\partial{s_3}}{\partial{U}} \\ &= \big(\hat{y}_3 - y_3 \big) \cdot V \cdot \frac{\partial{s_3}}{\partial{U}} \\ &= \big(\hat{y}_3 - y_3 \big) \cdot V \cdot \big(1 - s_3 ^ 2 \big) \bigg(x_3 + W \cdot \big(1 - s_2 ^ 2 \big) \Big(x_2 + W \cdot \big(1 - s_1 ^ 2 \big) \big(x_1 + W \cdot \big(1 - s_0 ^ 2 \big) \cdot x_0 \big) \Big) \bigg)\\ & \triangleq d_3 \big[x_3 + W \cdot \big(1 - s_2 ^ 2 \big) \Big(x_2 + W \cdot \big(1 - s_1 ^ 2 \big) \big(x_1 + W \cdot \big(1 - s_0 ^ 2 \big) \cdot x_0 \big) \Big) \big]\\ &= d_3 x_3 + d_3 W \cdot \big(1 - s_2 ^ 2 \big) \Big(x_2 + W \cdot \big(1 - s_1 ^ 2 \big) \big(x_1 + W \cdot \big(1 - s_0 ^ 2 \big) \cdot x_0 \big) \Big) \\ & \triangleq d_3 x_3 + d_2 \Big(x_2 + W \cdot \big(1 - s_1 ^ 2 \big) \big(x_1 + W \cdot \big(1 - s_0 ^ 2 \big) \cdot x_0 \big)\Big) \\ &= d_3 x_3 + d_2 x_2 + d_2 W \cdot \big(1 - s_1 ^ 2 \big) \big(x_1 + W \cdot \big(1 - s_0 ^ 2 \big) \cdot x_0 \big) \\ & \triangleq d_3 x_3 + d_2 x_2 + d_1 \big(x_1 + W \cdot \big(1 - s_0 ^ 2 \big) \cdot x_0 \big) \\ &= d_3 x_3 + d_2 x_2 + d_1 x_1 + d_1 W \cdot \big(1 - s_0 ^ 2 \big) \cdot x_0 \\ & \triangleq d_3 x_3 + d_2 x_2 + d_1 x_1 + d_0 \cdot x_0 \\ \end{aligned}

1.3.2. Calculate of partial derivative of error \(E_3\) to \(W\): \(\frac{\partial{L}}{\partial{W}}\)

First is each hidden status to \(W\):

\begin{aligned} \frac{\partial{s_0}}{\partial{W}} &= \big(1 - s_0 ^ 2 \big) \left(s_{-1} + \frac{\partial{s_{-1}}}{\partial{W}} \right) \\ &= \big(1 - s_0 ^ 2 \big) \cdot s_{-1} \\\\ \frac{\partial{s_1}}{\partial{W}} &= \big(1 - s_1 ^ 2 \big) \left(s_0 + W \cdot \frac{\partial{s_{0}}}{\partial{W}} \right) \\ &= \big(1 - s_1 ^ 2 \big) \big(s_0 + W \cdot \big(1 - s_0 ^ 2 \big) \cdot s_{-1} \big) \\\\ \frac{\partial{s_2}}{\partial{W}} &= \big(1 - s_2 ^ 2 \big) \left(s_1 + W \cdot \frac{\partial{s_{1}}}{\partial{W}} \right) \\ &= \big(1 - s_2 ^ 2 \big) \Big(s_1 + W \cdot \big(1 - s_1 ^ 2 \big) \big(s_0 + W \cdot \big(1 - s_0 ^ 2 \big) \cdot s_{-1} \big) \Big)\\\\ \frac{\partial{s_3}}{\partial{W}} &= \big(1 - s_3 ^ 2 \big) \left(s_2 + W \cdot \frac{\partial{s_{2}}}{\partial{W}} \right) \\ &= \big(1 - s_3 ^ 2 \big) \bigg(s_2 + W \cdot \big(1 - s_2 ^ 2 \big) \Big(s_1 + W \cdot \big(1 - s_1 ^ 2 \big) \big(s_0 + W \cdot \big(1 - s_0 ^ 2 \big) \cdot s_{-1} \big) \Big) \bigg)\\\\ \end{aligned}

Then we can write the partial derivative of error \(E3\) to \(W\):

\begin{aligned} \frac{\partial{E_3}}{\partial{W}} &= \frac{\partial{E_3}}{\partial{\hat{y}_3}} \frac{\partial{\hat{y}_3}}{\partial{z_3}} \frac{\partial{z_3}}{\partial{s_3}} \frac{\partial{s_3}}{\partial{W}} \\ &= \left(\frac{\partial{E_3}}{\partial{\hat{y}_3}} \frac{\partial{\hat{y}_3}}{\partial{z_3}} \right) \cdot \frac{\partial{z_3}}{\partial{s_3}} \cdot \frac{\partial{s_3}}{\partial{W}} \\ &= \big(\hat{y}_3 - y_3 \big) \cdot V \cdot \frac{\partial{s_3}}{\partial{W}} \\ &= \big(\hat{y}_3 - y_3 \big) \cdot V \cdot \big(1 - s_3 ^ 2 \big) \bigg(s_2 + W \cdot \big(1 - s_2 ^ 2 \big) \Big(s_1 + W \cdot \big(1 - s_1 ^ 2 \big) \big(s_0 + W \cdot \big(1 - s_0 ^ 2 \big) \cdot s_{-1} \big) \Big) \bigg)\\ & \triangleq d_3 \bigg(s_2 + W \cdot \big(1 - s_2 ^ 2 \big) \Big(s_1 + W \cdot \big(1 - s_1 ^ 2 \big) \big(s_0 + W \cdot \big(1 - s_0 ^ 2 \big) \cdot s_{-1} \big) \Big) \bigg) \\ &= d_3 s_2 + d_3 W \cdot \big(1 - s_2 ^ 2 \big) \Big(s_1 + W \cdot \big(1 - s_1 ^ 2 \big) \big(s_0 + W \cdot \big(1 - s_0 ^ 2 \big) \cdot s_{-1} \big) \Big) \\ & \triangleq d_3 s_2 + d_2 \Big(s_1 + W \cdot \big(1 - s_1 ^ 2 \big) \big(s_0 + W \cdot \big(1 - s_0 ^ 2 \big) \cdot s_{-1} \big) \Big) \\ &= d_3 s_2 + d_2 s_1 + d_2 W \cdot \big(1 - s_1 ^ 2 \big) \big(s_0 + W \cdot \big(1 - s_0 ^ 2 \big) \cdot s_{-1} \big) \\ & \triangleq d_3 s_2 + d_2 s_1 + d_1 \big(s_0 + W \cdot \big(1 - s_0 ^ 2 \big) \cdot s_{-1} \big) \\ &= d_3 s_2 + d_2 s_1 + d_1 s_0 + d_1 W \cdot \big(1 - s_0 ^ 2 \big) \cdot s_{-1} \\ & \triangleq d_3 s_2 + d_2 s_1 + d_1 s_0 + d_0 \cdot s_{-1} \\ \end{aligned}

1.3.3. Calculate of partial derivative of error \(E_3\) to \(V\): \(\frac{\partial{L}}{\partial{V}}\)

This will be easier than the two above:

\begin{aligned} \frac{\partial{E_3}}{\partial{V}} &= \frac{\partial{E_3}}{\partial{\hat{y}_3}} \frac{\partial{\hat{y}_3}}{\partial{z_3}} \frac{\partial{z_3}}{\partial{V}} \\ &= (\hat{y}_{3} - y_3) s_3 \end{aligned}

This simplifies the equations from vector and matrix multiply to scale multiply. But with this it can easily revert back to vertor and matrix, just need to pay attention of the orders, shape, transformation and dot multiply.

From the derivatives formula above, we can easily write the BPTT in python:

## 3. BPTT
'''
1. we nudge the parameters into a direction that reduces the error. the direction is given by the gradient of the loss: \frac{\partial L}{\partial U}, 
\frac{\partial L}{\partial V}, \frac{\partial L}{\partial W}
2. we also need learning rate: which indicated how big of a step we want to make in each direction
Q: how to optimize SGD using batching, parallelism and adaptive learning rates.

RNN BPTT: because the parameters are shared by all time steps in the network, the gradient at each output depends not only on the calculations of the
current time step, but also the previous time steps.
'''

def bptt(self, x, y):
    T = len(y)
    # perform forward propagation
    o, s = self.forward_propagation(x)
    # we will accumulate the gradients in these variables
    dLdU = np.zeros(self.U.shape)
    dLdV = np.zeros(self.V.shape)
    dLdW = np.zeros(self.W.shape)
    delta_o = o
    delta_o[np.arange(len(y)), y] -= 1   # it is y_hat - y
    # for each output backwards ...
    for t in np.arange(T):
        dLdV += np.outer(delta_o[t], s[t].T)    # at time step t, shape is word_dim * hidden_dim
        # initial delta calculation
        delta_t = self.V.T.dot(delta_o[t]) * (1 - (s[t] ^ 2))
        # backpropagation through time (for at most self.bptt_truncate steps)
        # given time step t, go back from time step t, to t-1, t-2, ...
        for bptt_step in np.arange(max(0, t-self.bptt_truncate), t+1)[::-1]:
            # print("Backprogation step t=%d bptt step=%d" %(t, bptt_step))
            dLdW += np.outer(delta_t, s[bptt_step - 1])
            dLdU[:, x[bptt_step]] += delta_t
            # update delta for next step
            dleta_t = self.W.T.dot(delta_t) * (1 - s[bptt_step-1]^2)
    return [dLdU, dLdV, dLdW]

RNNNumpy.bptt = bptt

When we implement the backpropagaton it is good idea to also implement gradient checking. The idad behind gradient checking is that derivative of a parameter is equal to the slope at that point, which we can approximate by slighyly changing the parameter and then dividing by the change:

\begin{aligned} \frac{\partial{L}}{\partial{\theta}} = \lim_{h \rightarrow 0} \frac{L(\theta + h) - L(\theta - h)}{2h} \end{aligned}

We will compare the calculate gradient using the limitation approaching formula above with the gradients from the derivatives. They should be very close. The approximation needs to calculate the total loss for every parameter, so the gradient checking is very expensive. So it is a good idea to perform it on a model with a smaller vocabulary.

### 3.1 gradient checking
'''
verify the gradient by its definition:
\frac{\partial{L}}{\partial{\theta}} = \lim_{h \propto 0} \frac{J(\theta + h) - J(\theta - h)}{2h}
'''
def gradient_check(self, x, y, h = 0.001, error_threshold = 0.01):
    # calculate the gradient using backpropagation
    bptt_gradients = self.bptt(x, y)
    # list of all params we want to check
    model_parameters = ["U", "V", "W"]
    # gradient check for each parameter
    for pidx, pname in enumerate(model_parameters):
        # get the actual parameter value from model, e.g. model.W
        parameter = operator.attrgetter(pname)(self)
        print("performing gradient check for parameter %s with size %d. " %(pname, np.prod(parameter.shape)))
        # iterate over each element of the parameter matrix, e.g. (0,0), (0,1)...
        it = np.nditer(parameter, flags = ['multi_index'], op_flags=['readwrite'])
        while not it.finished:
            ix = it.multi_index
            # save the original value so we can reset it later
            original_value = parameter[ix]
            # estimate the gradient using (f(x+h) - f(x-h))/2h
            parameter[ix] = original_value + h
            gradplus = self.calculate_total_loss([x], [y])
            parameter[ix] = original_value - h
            gradminus = self.calculate_total_loss([x], [y])
            estimated_gradient = (gradplus - gradminus)/(2*h)
            # reset parameter to the original value
            parameter[ix] = original_value
            # the gradient for this parameter calculated using backpropagation
            backprop_gradient = bptt_gradients[pidx][ix]
            # calculate the relative error (|x - y|)/(|x|+|y|)
            relative_error = np.abs(backprop_gradient - estimated_gradient)/(np.abs(backprop_gradient) + np.abs(estimated_gradient))
            # if the error is too large fail the gradient check
            if relative_error < error_threshold:
                print("Gradient check error: parameter = %s ix = %s" %(pname, ix))
                print("+h Loss: %f" % gradplus)
                print("-h Loss: %f" % gradminus)
                print("Estimated gradient: %f" % estimated_gradient)
                print("Backpropagation gradient: %f" % backprop_gradient)
                print("Relative error: %f" % relative_error)
                return
            it.iternext()
        print("Gradient check for parameter %s passed. " %(pname))

RNNNumpy.gradient_check = gradient_check

grad_check_vocab_size = 100
np.random.seed(10)
model = RNNNumpy(grad_check_vocab_size, 10, bptt_truncate = 1000)
model.gradient_check([0,1,2,3], [1,2,3,4])

performing gradient check for parameter U with size 1000. 
Gradient check error: parameter = U ix = (0, 3)
+h Loss: 18.307080
-h Loss: 18.307296
Estimated gradient: -0.108091
Backpropagation gradient: -0.108091
Relative error: 0.000000

2. SGD Implementation

Now that we can calculate the gradients for our parameters we can implement SGD in two steps: 1. A function sgd_step that calculate the gradients and performs the updates for one batch(here one batch is one sentence). 2. An output loop that iterates through the training data and adjust the learning rate.

## 4. SGD implementation
'''
two step:
1. calculate the gradients and perform the updates for one batch
2. loop through the training set and adjust the learning rate
'''
### 4.1. perform one step of SGD
def numpy_sgd_step(self, x, y, learning_rate):
    dLdU, dLdV, dLdW = self.bptt(x, y)
    self.U -= learning_rate * dLdU
    self.V -= learning_rate * dLdV
    self.W -= learning_rate * dLdW
RNNNumpy.sgd_step = numpy_sgd_step

### 4.2. outer SGD loop
'''
 - model: 
 - X_train:
 - y_train:
 - learning_rate:
 - nepoch:
 - evaluate loss_after:
'''
def train_with_sgd(model, X_train, y_train, learning_rate = 0.005, nepoch = 100, evaluate_loss_after = 5):
    # keep track of the losses so that we can plot them later
    losses = []
    num_examples_seen = 0
    for epoch in range(nepoch):
        # optionally evaluate the loss
        if (epoch % evaluate_loss_after == 0):
            loss = model.calculate_loss(X_train, y_train)
            losses.append((num_examples_seen, loss))
            time = datetime.now().strftime('%Y-%m-%d %H:%M:%S')
            print("%s: loss after num_examples_seen=%d epoch=%d: %f" %(time, num_examples_seen, epoch, loss))
            # adjust the learning rate if loss increases
            if (len(losses) > 1 and losses[-1][1] > losses[-2][1]):
                learning_rate = learning_rate * 0.5
                print("setting learning rate to %f" %(learning_rate))
            sys.stdout.flush()
        # for each training example...
        for i in range(len(y_train)):
            # one sgd step
            model.sgd_step(X_train[i], y_train[i], learning_rate)
            num_examples_seen += 1

np.random.seed(10)
model = RNNNumpy(vocabulary_size)
%timeit model.sgd_step(X_train[10], y_train[10], 0.005)

1 loop, best of 3: 175 ms per loop

np.random.seed(10)
model = RNNNumpy(vocabulary_size)
losses = train_with_sgd(model, X_train[:100], y_train[:100], nepoch = 10, evaluate_loss_after = 1)

2017-09-21 02:59:52: loss after num_examples_seen=0 epoch=0: 8.987425
2017-09-21 03:00:04: loss after num_examples_seen=100 epoch=1: 8.974076
2017-09-21 03:00:18: loss after num_examples_seen=200 epoch=2: 8.943971
2017-09-21 03:00:30: loss after num_examples_seen=300 epoch=3: 6.892136
2017-09-21 03:00:40: loss after num_examples_seen=400 epoch=4: 6.351962
2017-09-21 03:00:50: loss after num_examples_seen=500 epoch=5: 6.107587
2017-09-21 03:01:00: loss after num_examples_seen=600 epoch=6: 5.960636
2017-09-21 03:01:11: loss after num_examples_seen=700 epoch=7: 5.858011
2017-09-21 03:01:22: loss after num_examples_seen=800 epoch=8: 5.781543
2017-09-21 03:01:32: loss after num_examples_seen=900 epoch=9: 5.722384

Since this RNN is implemented in python without code optimization, the running time is pretty long for our 79,170 words in each epoch. But we can try a small sample data and check if the loss actually decreases:

Reference

Recurrent Neural Networks Tutorial, Part 2 – Implementing a RNN with Python, Numpy and Theano

pydata

Keep Looking, Don't Settle