pydata

Keep Looking, Don't Settle

Numpy Introduction 03

0. Introduction

Continue to introduce a little about numpy following Numpy Introduction 01 and Numpy Introduction 02

  1. np.ndarray basics
  2. np.ndarray structure
  3. slicing, masking, fancy indexing and broadcasting

1. 矩阵的元素，维度和内存大小

alt text

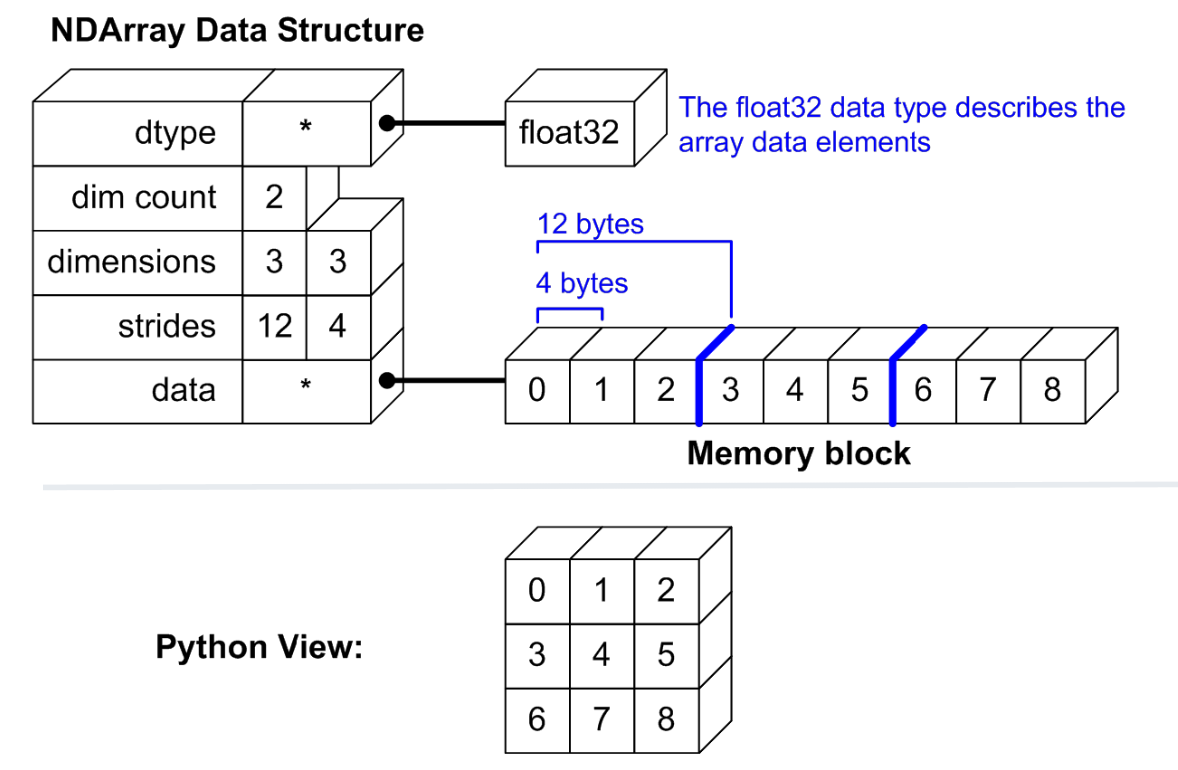
import numpy as np

x=  np.arange(2*3*2*4).reshape(2,3,2,4).astype('int32')
print("type of x is : " + str(type(x)))

type of x is : <type 'numpy.ndarray'>

# 不同的的dtype占用的内存大小不一样
print("dtype of x is : "+ str(x.dtype))

dtype of x is : int32

# x的维数,是一个4维的矩阵
print("x是一个4维矩阵,所以维度是: " + str(x.ndim))

x是一个4维矩阵,所以维度是: 4

#shape表示在每个维度上有多少个元素(item)
print("x是一个4维矩阵,每个维度上item的个数为: " + str(x.shape))

x是一个4维矩阵,每个维度上item的个数为: (2, 3, 2, 4)

# size表示总共有多少个元素(所有维度上shape的和)
print("x总共有多少个item: " + str(x.size) + ": = 2x3x2x4")

x总共有多少个item: 48: = 2x3x2x4

# 每一个item占用的内存的大小，int16是2bytes，int32是4bytes，float64是8bytes
print("每一个item占用的内存的大小: " + str(x.itemsize) + " bytes")

每一个item占用的内存的大小: 4 bytes

# np.ndarray所有item占用的总共内存
print("所有item占用的总共内存: " + str(x.nbytes) + " bytes")

所有item占用的总共内存: 192 bytes

print(x.strides)

(96, 32, 16, 4)

2. 矩阵的排列

numpy采用和C, java相似的方法：

  1. 首先横着排(列优先，所以任何时候列总是最后一个维度，即-1维总是列)，np.arange(4)是一个行向量，占据4个列，shape为(4, ), shape[-1] = 4

  2. 增加一个维度以后变成2维的，增加的维度在shape上的表现是加在左边，在矩阵上的表现是增加了行. np.arange(2*4).reshape(2,4)是一个2行4列的矩阵。每一行在内存里面是相连的

  3. 再增加一个维度以后变长3维的，增加的维度在shape上的表现是加在最左边，在矩阵上的表现是增加了depth. np.arange(3*2*4).reshape(3, 2, 4)是depth为3，每个depth上是一个2行4列的矩阵

  4. 4d的时候，可以假想basic unit是3d的cube，然后把它们连成一行排起来，变成4d

  5. 同样，5d可以认为是在4d的基础上向下增加行，6d可以认为再增加depth，等等

总之：np.ndarray 的-1维度(最后一个维度)总是column，倒数第二个维度是行，倒数第三个维度是depth，

2.1. First will occupy columns(one dimension)

alt text

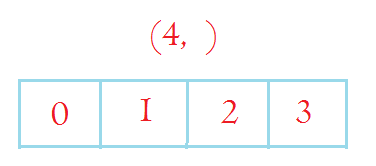
np.arange(4)

array([0, 1, 2, 3])
2.2. second will be row (down, two dimensions)

alt text

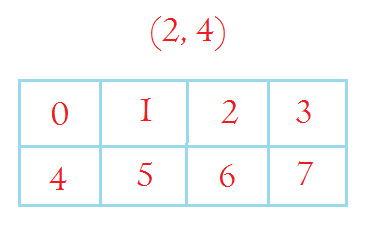
np.arange(8).reshape(2, 4)

array([[0, 1, 2, 3],
       [4, 5, 6, 7]])
2.3. third will be depth direction (3 dimensions, 3 arrays each shape is 2x4)

alt text

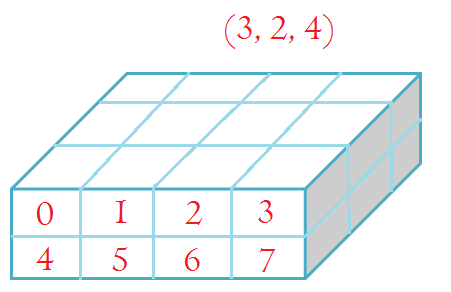
np.arange(24).reshape(3, 2, 4)

array([[[ 0,  1,  2,  3],
        [ 4,  5,  6,  7]],

       [[ 8,  9, 10, 11],
        [12, 13, 14, 15]],

       [[16, 17, 18, 19],
        [20, 21, 22, 23]]])
2. 4. forth will be column blocks, each block is 3 dimension arrays

alt text

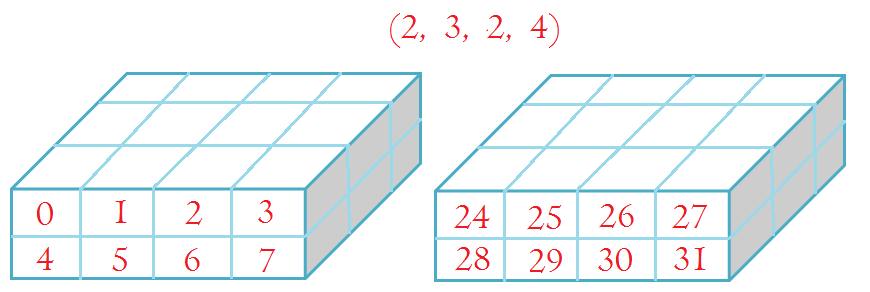
np.arange(48).reshape(2, 3, 2, 4)

array([[[[ 0,  1,  2,  3],
         [ 4,  5,  6,  7]],

        [[ 8,  9, 10, 11],
         [12, 13, 14, 15]],

        [[16, 17, 18, 19],
         [20, 21, 22, 23]]],


       [[[24, 25, 26, 27],
         [28, 29, 30, 31]],

        [[32, 33, 34, 35],
         [36, 37, 38, 39]],

        [[40, 41, 42, 43],
         [44, 45, 46, 47]]]])

3. Slicing, Masking, Fancy Indexing and Broadcasting

  1. slicing: like slicing in python list, e.g. x[3:6]. Slicing is a reference, not a copy.
  2. masking: use boolean array indexing, e.g. x[x > 2]
  3. fancy indexing: pass a list/array of indices, x[[1,3,5]]
  4. broadcasting: a set of rules for array calculation with different dimension or shape size. broadcasting可以避免某些for循环，从而大大增加计算速度。

Broadcasting is a set of rules by which ufuncs operate on arrays of different sizes and/or dimensions.

Broadcasting rules: 1. 如果两个array的ndim不一样，那么会在ndim比较小的array左边垫上1(类似newaxis)直到两个array的ndim一样 2. 两个array在所有的dim上必须满足：要么在每一维度上size相同，要么size为1(size=1的array在其维度上会类似copy的方式把它展开到跟另一个矩阵相同size) 3. broadcasting得到的array的shape是原来两个矩阵在各个维度上的shape的最大值

3.1. An example of Broadcasting

使用broadcasting的一个例子，nearest neighbour: x0是一个100x3的矩阵，表示100个点，现在要求对这100个点里面的每一个给定的点，另外99个点里面哪个点跟这个给定的点欧氏距离最近。

np.random.seed(9)
x0 = np.random.normal(0, 1, 300).reshape(100, 3)
print(x0.shape)

(100, 3)

下面使用broadcasting来计算距离，这样可以避免for循环。

首先把100x3的矩阵reshape成100x1x3(e.g., x0.reshape(100, 1, 3))，变成一个depth为100，一行3列的矩阵。这个矩阵减去原来100行3列的矩阵，根据broadcasting的规则，它会这么做：

  1. 首先把ndim较小的矩阵在最左边增加一维，变成1x100x3，然后相减。这时候第一个矩阵在行上的size只有1，会被copy层成100(不是真正的copy，这儿只是借用copy这个说法)，所以第一个矩阵变成100x100x3。同样第一个矩阵1x100x3，也会在它的depth上被copy100次变成100x100x3。

  2. 这样的结果就是初始的100x3的矩阵每一行都会跟这100x3的矩阵相减

  3. 最后得到的结果矩阵是100x100x3。

diff = x0.reshape(100, 1, 3) - x0
print(diff.shape)

(100, 100, 3)

distance = np.square(diff).sum(axis = -1)
i = np.arange(100)
distance[i, i] = np.inf

ind = np.argmin(distance, axis = 1)
print(ind[:10])

[73 22 11 21 21 71 28 28 41 31]

这样的结果跟sklearn的NearestNeighbors得到的结果相同:

from sklearn.neighbors import NearestNeighbors
dist_sk, ind_sk = NearestNeighbors().fit(x0).kneighbors(x0, 2)
print(ind_sk[:10, 1])

[73 22 11 21 21 71 28 28 41 31]

同样由上面我们也看到broadcasting的一个问题：大大增加了内存的使用。原来一个100x3的矩阵因为broadcasting，最后大小增加了100倍。如果矩阵的shape很大的时候，这样会消耗很多的内存。最后导致速度可能更慢而不是更快。

References

  1. Broadcasting
  2. Array Broadcasting in numpy