pydata

Keep Looking, Don't Settle

SVM Introduction

Intro

We have two classes of data, the + and the -. Now if there is an unknown point \(\vec{u}\), shall we classify it as + or -?

Alt text

1) suppose there is a line that can split the + and the -(the dashed line). We project \(\vec{u}\) to the direction perpendicular to the split line, that is, the direction of \(\vec{\omega}\).

Then the decition rule is:

If projection length \(\vec{\omega} \cdot \vec{u} \ge c\), then +

if projection length \(\vec{\omega} \cdot \vec{u} \le c\), then -

let \(b = -c\), then we have the decision rule is \(\vec{\omega} \cdot \vec{u} + b \ge 0\), then +.

Now we need to find \(\vec{\omega}\) and \(b\) (the parameters to decide the dashed line).

2) Next, for given + and - samples, we want

\begin{aligned} \vec{\omega} \cdot \vec{x}_ {+} + b \ge 1 \mbox{ , right solid line} \\ \vec{\omega} \cdot \vec{x}_ {-} + b \le -1 \mbox{ , left solid line} \end{aligned}

For math convenience, we define \(y_i\) s.t.

\begin{aligned} y_i = \left\{ \begin{array}{lr} 1, \mbox{ for + sample} \\ -1, \mbox{ for - sample} \\ \end{array} \right. \end{aligned}

So we have

\(y_i (\vec{\omega} \cdot \vec{x}_ {+} + b) \ge 1\), that is,

\(y_i (\vec{\omega} \cdot \vec{x}_ {+} + b) - 1 \ge 0\) for all + samples.

Then for the points on the boundary, we have \(y_i (\vec{\omega} \cdot \vec{x}_ {+} + b) - 1 = 0\).

We want the street(distance between two solid line) to be as wide as possible.

The width is \((\vec{x}_ {+} - \vec{x}_ {-})\) projected on the unit direction vector. So the length is

\begin{aligned} (\vec{x}_ {+} - \vec{x}_ {-}) \cdot \frac{\vec{\omega}}{||\vec{\omega}||} = \frac{2}{||\vec{\omega}||} \end{aligned}

The following are equvalent:

\begin{aligned} \mbox{max} \frac{2}{||\vec{\omega}||} \Leftrightarrow \mbox{min} ||\vec{\omega}|| \Leftrightarrow \mbox{min} \frac{1}{2} ||\vec{\omega}||^{2} \end{aligned}

Use Lagrange multipliers,

\begin{aligned} L = \frac{1}{2} ||\vec{\omega}||^{2} - \sum_{i} \alpha_i \left[ y_i (\vec{\omega} \cdot \vec{x} + b) - 1 \right] \end{aligned}

For \(\vec{x}\) not on the boundary, $\alpha_i $ will be 0. So only the points on the boundary will play role in.

The floowing is an example to show how the boundary points are used in building the linear separater.

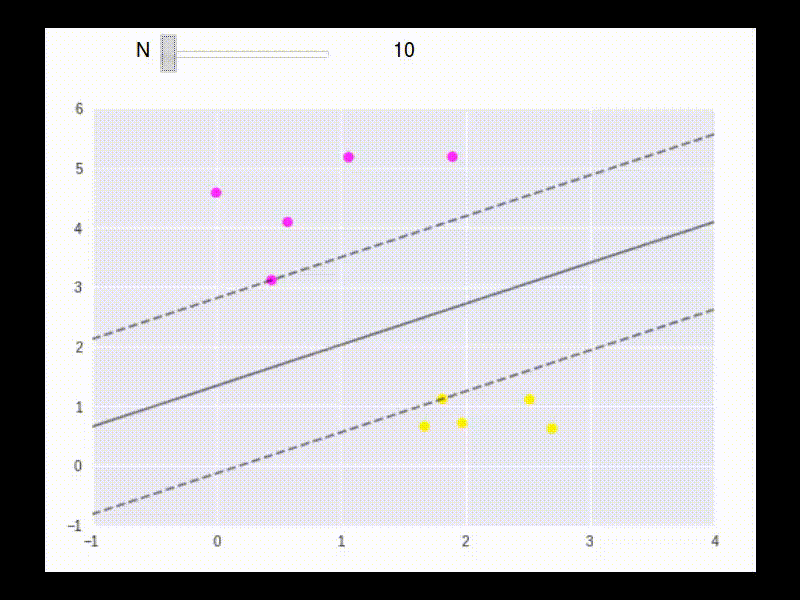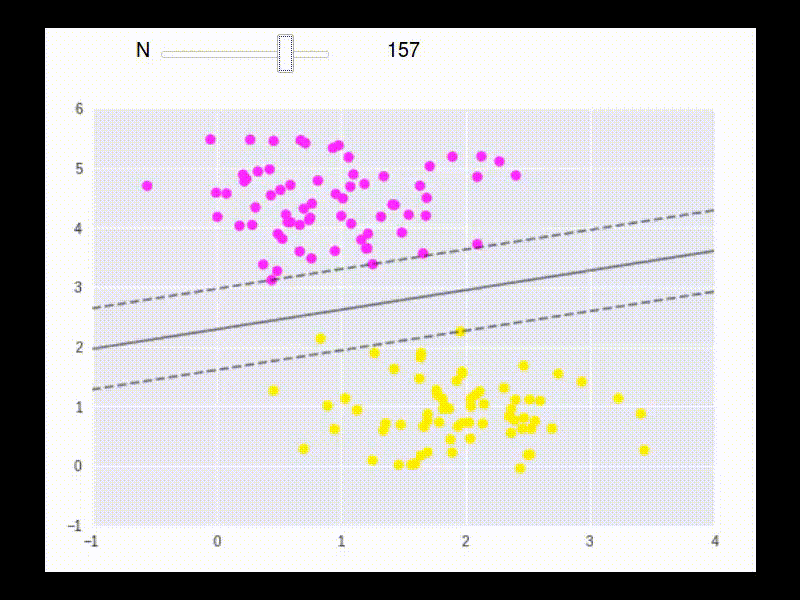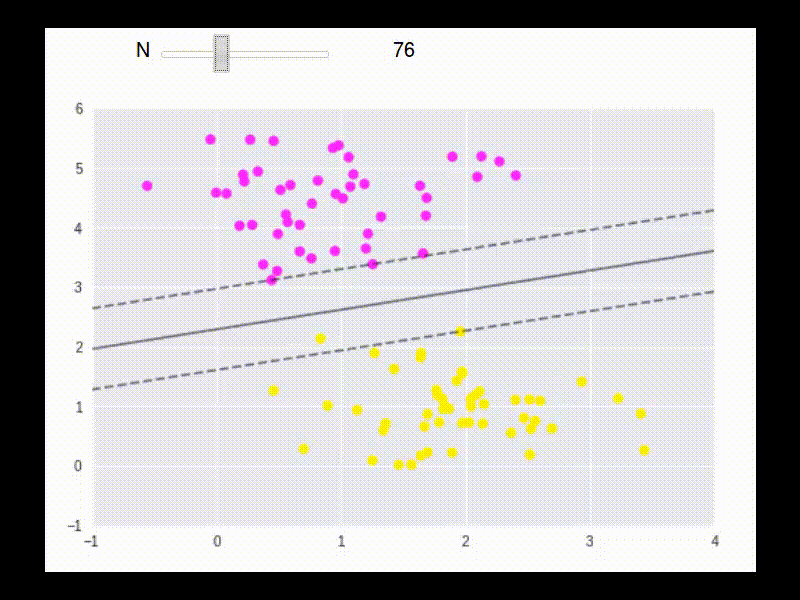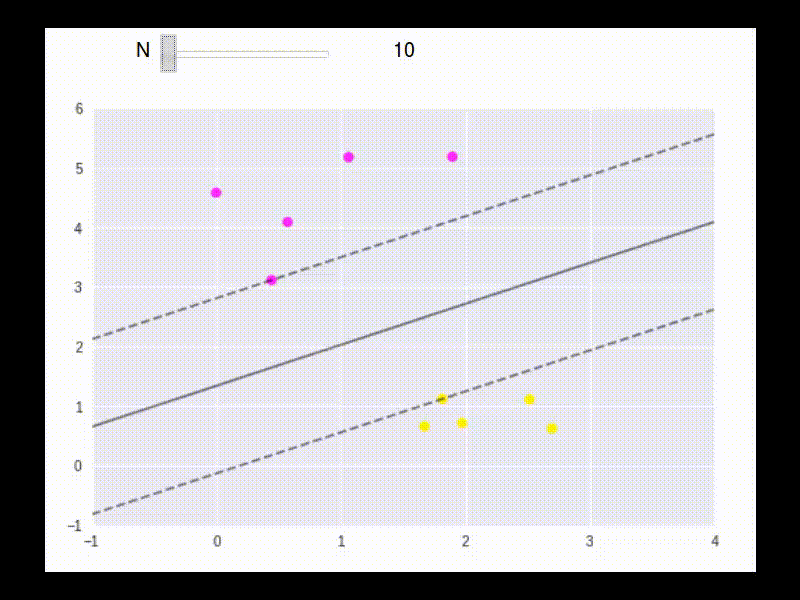
Alt text

To max \(L\), take partial derivatives:

\begin{aligned} \frac{\partial{L}}{\partial{\vec{\omega}}} = \vec{\omega} - \sum_{i} \alpha_{i} y_{i} \vec{x}_ {i} \end{aligned}

So we have

$$\vec{\omega} = \sum_{i} \alpha_{i} y_{i} \vec{x}_ {i} $$

So, \(\vec{\omega}\) is a linear sum of the vectors \(\sum_ {i} \alpha_ {i} y_ {i} \vec{x}_ {i}\). Since some \(\alpha_ {i}\) will be 0, so, \(\vec{\omega}\) is only some of the vectors sum.

Take partial derivative to \(b\), we have:

\begin{aligned} \frac{\partial{L}}{\partial{b}} = - \sum_{i} \alpha_{i} y_{i} \end{aligned}

So, \(\sum_{i} \alpha_{i} y_{i} = 0\). This is a quadratic optimization problem.

Plug in \(\vec{\omega}\) into \(L\), we will have

\begin{aligned} L = \frac{1}{2} \left(\sum_{i} \alpha_{i} y_{i} \vec{x}_ {i} \right) \left(\sum_ {i} \alpha_{i} y_{i} \vec{x}_ {i} \right) - \sum_{i} \alpha_{i} y_{i} \vec{x}_{i} \cdot \left(\sum_{i} \alpha_{i} y_{i} \vec{x}_ {i} \right) - \sum_{i} \alpha_{i} y_{i} b + \sum_{i} \alpha_{i} \end{aligned}

Since we have \(\sum_{i} \alpha_{i} y_{i} = 0\), So,

\begin{aligned} L = \sum_{i} \alpha_{i} - \frac{1}{2} \sum_{i} \sum_{j} \alpha_{i} \alpha_{j} y_ {i} y_ {j} \vec{x}_ {i} \cdot \vec{x}_ {j} \end{aligned}

So the max of \(L\) only depends on the pairs of \(\vec{x}_ {i} \cdot \vec{x}_ {j}\).

Plug in \(\vec{\omega}\) into the decision rule, we have

\begin{aligned} \sum_{i} \alpha_ {i} y_ {i} \vec{x}_ {i} \cdot \vec{u} + b \ge 0, \mbox{then +} \end{aligned}

it is also the vector product.

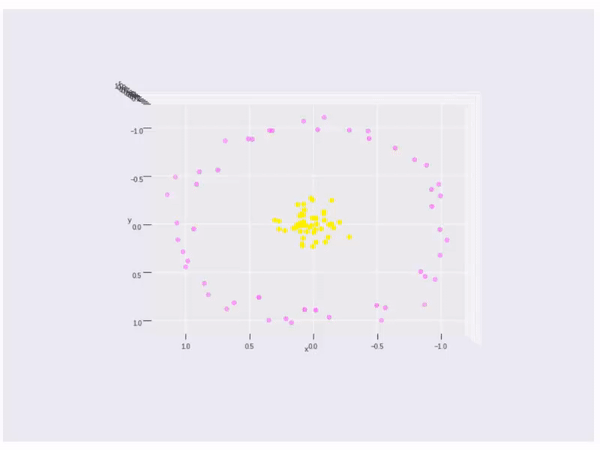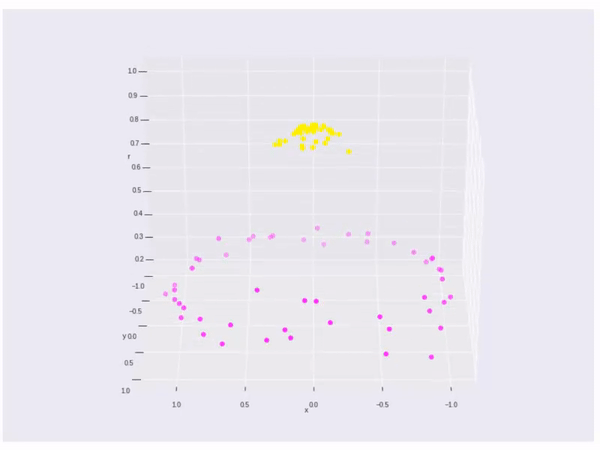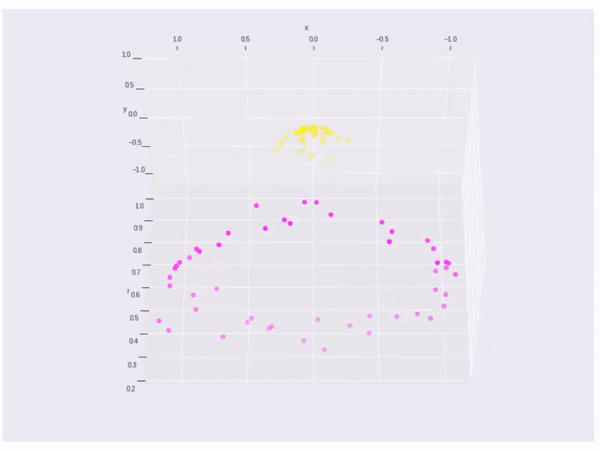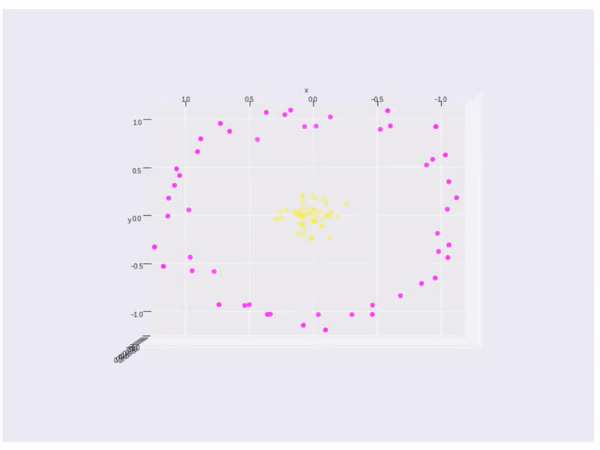
A little more, if the data cannot be splited by a linear line or linear space, what shall we do? Like the data points below, there is no linear method can split the data.

Alt text

If the data cannot split by a linear line, then we will change vector \(\vec{x}\) to a kernel function \(\phi(\vec{x})\). So we need \(\phi(\vec{x}_ {i}) \cdot \phi(\vec{x}_ {j})\) to max. The kernel is

\begin{aligned} k\left( \vec{x}_ {i}, \vec{x}_ {j}\right) = \phi(\vec{x}_ {i}) \cdot \phi(\vec{x}_ {j}) \end{aligned}

So what I need is the kernel function \(k\) to map \(\vec{x}_ {i} \vec{x}_ {j}\) to another space.

Choice of \(k\):

1) \(\left(\vec{x}_ {i} \vec{x}_ {j} + 1 \right)^{n}\)

2) \(e^{\frac{||\vec{x}_ {i} - \vec{x}_ {j}||}{\sigma}}\)

Finally, it is an example of kernel function to visualize the second kernel above(rbf kernel):

Alt text