The purpose of recommendation system is to recommend the related products (item) to the users based on the user's query.
1. Terminology
1.1. Items (also known as documents)
The entities a system recommends. For the Google Play store, the items are apps to install. For YouTube, the items are videos.
1.2. Query (also known as context)
The information a system uses to make recommendations. Queries can be a combination of the following:
user information
the id of the user items that users previously interacted with
additional context
time of day the user's device
目的就是把item推荐给user based on user information.
1.3. Embedding
A mapping from a discrete set (in this case, the set of queries, or the set of items to recommend) to a vector space called the embedding space. Many recommendation systems rely on learning an appropriate embedding representation of the queries and items.
2. Recommendation Systems Overview
2.1. Candidate Generation / Retrival
In this first stage, the system starts from a potentially huge corpus and generates a much smaller subset of candidates. For example, the candidate generator in YouTube reduces billions of videos down to hundreds or thousands. The model needs to evaluate queries quickly given the enormous size of the corpus. A given model may provide multiple candidate generators, each nominating a different subset of candidates.
2.2. Scoring
Next, another model scores and ranks the candidates in order to select the set of items (on the order of 10) to display to the user. Since this model evaluates a relatively small subset of items, the system can use a more precise model relying on additional queries.
2.3. Re-ranking
Finally, the system must take into account additional constraints for the final ranking. For example, the system removes items that the user explicitly disliked or boosts the score of fresher content. Re-ranking can also help ensure diversity, freshness, and fairness.
We will discuss each of these stages over the course of the class and give examples from different recommendation systems, such as YouTube.
3. Candidate Generation Overview
1. content-based filtering: recommendate based on the similarity of items
2. collaborative filtering: if user A and user B are similar, then recommend user A's items to user B.
3.1. Embedding Space: map item and query to a \(d\) dimension space
Map each item and each query (or context) to an embedding vector in a common embedding space . Typically, the embedding space is low-dimensional \(E = \mathbb{R}^{d}\) (that is, is much smaller than the size of the corpus), and captures some latent structure of the item or query set.
3.2. Similarity Measures:based on embedding to find item, or find the related items and querys
A similarity measure is a function \(s: E X E -> \mathbb{R}\) that takes a pair of embeddings and returns a scalar measuring their similarity. The embeddings can be used for candidate generation as follows: given a query embedding \(q \in E\), the system looks for item embeddings \(x \in E\) that are close to \(q\), that is, embeddings with high similarity \(s(q, x)\).
\(cos(x,y)\): the anger between two vectors. Below C and item has the least anger degree.
\(dot(x, y)\):dot product, the length of vector 1 times the length of vector 2, then times cos(anger). A is the longest.
Eculidian distance ||x - y||: which is the distance of two vectors. B and query has the shortest dist.
3.3. Which Similarity Measure to Choose?
If use dot prod, the bigger the norm of the vector, the more likely it will be selected. The item has more frequency are usually have embedding with bigger norm, which will result in the common items (or most viewed videos) are more likely to be recommended.
4. Content-based Filtering
Which recommend based on similar items. Ignore here sicne it is easy.
5. Collaborative Filtering
5.1. Basics
Take an example to recommend movies to the customer. One row is one customer, and one column is one movie. The target is: for a given customer, recommend movies to him based on the customers that are clsoe to him.
Suppose movies has these features: name, rating, introduction
5.1.1. 1-d embedding
Suppose we can score the movie from -1 to 1 based on if it is for kids or for adults. -1 means for kids and 1 means only for adults. With this each movie will have a score from -1 to 1. In the same way, we can score the customers based on they are kids or adults.
Now in the (user,item) feedback matrix we have the "like" from the user to the movie.
5.1.2. 2-d embedding
Most of the time, 1-d cannot describe the complexity of the movie. We may need 2-d or high dimension to describe. Suppose we have another dimenison to describe the movie is Arthose or Blockbuster.
5.2. Matrix Factorization
Assume feedback matrix \(A \in \mathbb{R}^{m \times n}\), m x n matrix. m means m user, and n means n items.
Matrix Factorization is to get a matrix U and matrix V, such that
1. U is matrix m x d, each row is an user's embedding
2. V is matrix n x d, each row is an item's embedding
Our goal is to factorize the ratings matrix \(A\) into the product of a user embedding matrix \(U\) and movie embedding matrix \(V\), such that \(A \approx UV^\top\) with
Here
- $N$ is the number of users,
- $M$ is the number of movies,
- $A_{ij}$ is the rating of the $j$th movies by the $i$th user,
- each row $U_i$ is a $d$-dimensional vector (embedding) representing user $i$,
- each row $V_j$ is a $d$-dimensional vector (embedding) representing movie $j$,
- the prediction of the model for the $(i, j)$ pair is the dot product $\langle U_i, V_j \rangle$.
embedding matrix U and V has \(UV^T\) as approx of feedback matrix A. A has dim \(m \times n\), the new U V has dim = \((m+n)\times d\). Usually d is small, which means we will use low dim matrix to approx the original A. Singular value decomposion (SVD) is not a good method here because A is sparse most of the time.
1. Stochastic gradient descent (SGD) is a generic method to minimize loss functions.
2. Weighted Alternating Least Squares (WALS) is specialized to this particular objective.
1. pros: no special pre-knowledge, Serendipity (model help to get likes), easy to start
2. cons: cannot handle new item, cannot use side features (age, address)- high dim feedback matrix A
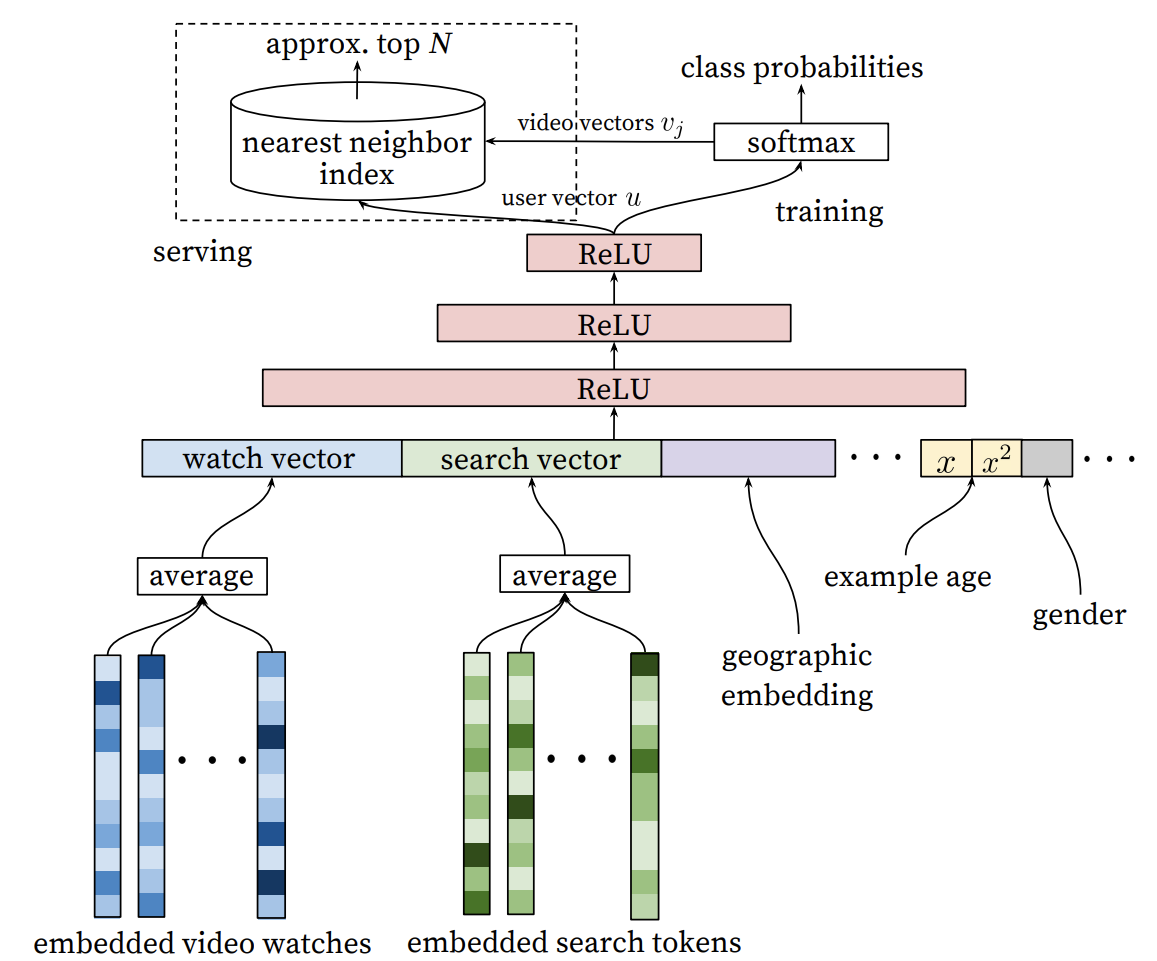
6. Recommendation with Deep Neural Network (DNN) Models
DNN can put item feature and user feature into a network modle to learn embeddings.
Softmax DNN for Recommendation
input: user query
output: prob of n items
input X can be dense feature (watch time length, time since last watch), it can also be sparse feature (country, watch history).
Last hidden layer of DNN output is \(\phi(x)\), which is a vector with dim = d. It will times a matrix V \(V \in n \times d\) to get a vector with dim = n. Each value is the probability for item.
Loss funciton is the function of model output \(\hat{p}\) and the true item y. We can use cross entropy.
The purpose of the model is to learn embedding, s.t. for each item j, there is an vector \(v_j \in \mathbb{R}^d\) (n items, then \(V \in n \times d\)). With softmax model, V are the parameters of the model.
For query embedding, for query i, model is not to get embedding \(U_{i}\), but to learn the function \(\phi(\cdot)\), which will map input x to a d-dim vector \(\phi(x)\)
Furthermore, can we build two DNN: 1. 1st DNN is to get function \(\phi(x_{item}) \in \mathbb{R}^{d}\), map item to d-dim space 2. 2nd DNN is to get funciton \(\psi(x_{query}) \in \mathbb{R}^{d}\), map query to d-dim space
Finally we can use dot product < \(\phi(x_{item})\), \(\psi(x_{query})\) > to get the correlation between query i and item j.
Train the model
The training data includes the user's query and the user's side features, and the items that the user has been interested before for each user. The forward and backward propagation is based on the design of the DNN. The minium of the loss funciton can be achieved by stochastic gradient descending algorithm.
Negative sampling
When there are n items, the output prob from DNN is \(\hat{p} \in \mathbb{R}^{n}\). Since n is very big, which will result in lots of calcualation in backpropagation.(In NLP, when clac the prob of neighbors words given the central word, it also uses negative smapling because of word size is also very big).
Negative sampling will do:
1. All positive items (the ones that appear in the target label)
2. A sample of negative items (j in 1, 2, 3, ... n)
An example from Youtube recommendation: