1. What the problem to solve?

春节回去的时候正好碰上DeepSeek发布新的模型，一时间各路媒体讨论的沸沸扬扬，几乎上升到国运的高度。讨论的最重要的应该是两点：第一个是媲美其他主流模型的benchmark分数；第二个是说训练速度快了很多，使用了少的多的GPU时间。可是各路讨论多是繁华之论以及振奋人心的消息，而没有具体的DS为什么好，怎么好的。回来的第一个周末，花了周末的时间读了一下DS V3的论文。之所以选择V3因为R1是之于V3进行了RL和SFT来增强模型的推理能力，基本的模型还是V3，而且DS V3的论文也更详细。文章的第二部分讲述了DS在模型的架构上（science）有一些什么样的改进，第三部分讲述了在模型的训练上（engineering）有什么改进，然后两部分讲了pretraining和posttraining以及evaluation相关的东西。

2. How to solve / Model architecture?

2.1. Basic Architecture

模型的基本架构里面主要有两点：1是把原来的Attention改成了Multi-head Latent Attention；2是把原来的FFN改成了DeepSeekMoE。这样做的目的一是减少了计算量；二是减少了cache的data，从而节约了GPU的内存。具体如下：

DeekSeek模型架构

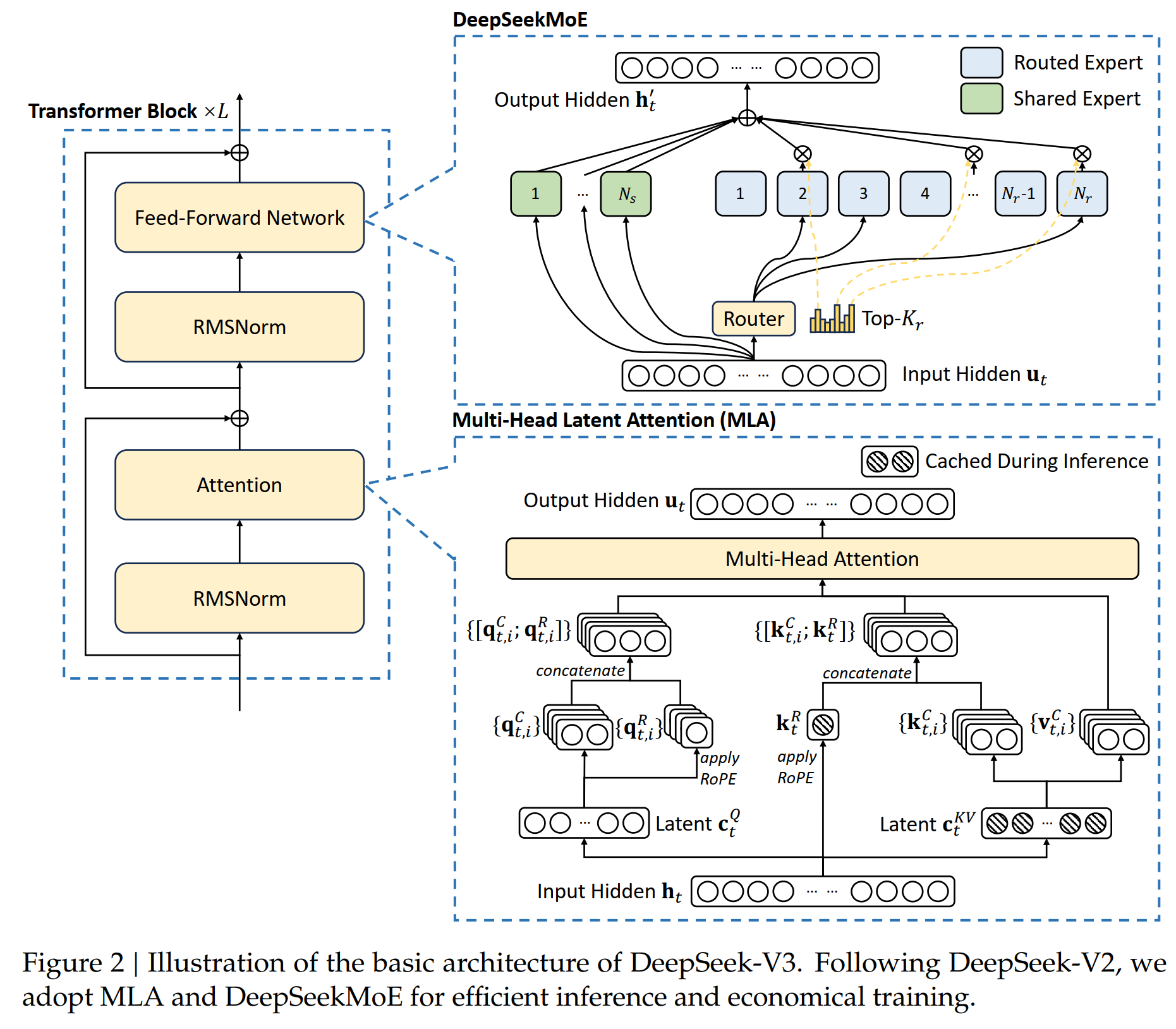
2.1.1. Multi-head latent attention (MLA)

相比较于原始的Attention模型里面介绍的注意力机制, DS使用Multi-head latent attention (MLA)的架构，跟原来的Multi-head attention不一样的是这里面从 $h_t$ 来计算 $k,q,v$ 的时候，先进行降维，把 $h_t\in {\mathbb{R}}^d$ 投影到一个低维空间 $\text{textcolor}blue{c}_t^{KV}=W^{DKV}{h}_t$ ，然后再升维到 $\text{textcolor}blue{k}_t^C=W^{UK}{c}_t^{KV}$ ；以及投影到一个低维的 $\text{textcolor}blue{c}_t^Q=W^{DQ}{h}_t$，然后再升维到 $\text{textcolor}blue{q}_t^C=W^{UQ}{c}_t^Q$。这样的话在进行inference的时候只要保存低维的 $\text{textcolor}blue{c}_t^{KV}$ 和 $\text{textcolor}blue{c}_t^Q$. 比如说，原来的 $\text{dim}(h_t)=7168$, 通过一个降维矩阵 $\text{dim}(W^{DKV})=4096\times 7186$把它降到4096维，那么需要保存的矩阵 $\text{textcolor}blue{c}_t^{KV}$就小了很多。 具体地说，

这里 $W^{DKV}\in {\mathbb{R}}^{d_c\times d}$ 是一个降维投影矩阵; $W^{UK},W^{UV}\in {\mathbb{R}}^{d_h{n}_h\times d_c}$ 是对应的 keys 和 values 的升维矩阵。在做inference的时候，只需要$\text{textcolor}blue{c}_t^{KV}$和$\text{textcolor}blue{k}_t^R$，即节省了计算量，也节约了内存。

对Query，也有同样的处理来降维

2.1.2. DeepSeekMoE with Auxiliary-Loss-Free Load Balancing

Basic Architecture of DeepSeekMoE

在2017年的Attention论文里面，decoder先是计算Attention，然后再计算FFN从而predict最后的token。DS里面，FFN被进一步改成了MoE。MoE的意思是模型是由一些列的Expert构成。每个Expert可以是一个MLP，一个CNN或者其他的神经网络模型，或者每个Expert可以是一个tansformer的encoder/decoder。每个 Expert 负责学习不同的数据模式，MoE 通过 Gating Network 选择合适的Expert，使得不同的数据被送往最擅长Expert家处理。每预测下一个token的时候，MoE不是使用某一个Expert，也不是使用所有的Expert，而是选择其中的Top $K$ 个Expert来进行预测。选哪 $K$ 个Expert是通过一个Gating网络来确定。通常 $K\ll N$，所以MoE是一个稀疏网络。使用MoE第一个好处是通过更精细化的划分，模型有更大的灵活性，不同的Expert可以学习不同的数据。比如如果 $N=16$，$K=2$，那么就有 $C(16,2)=160$ 个组合。如果每个Expert再split成4个小的Expert，那么总共的组合就是 $C(64,8)=4,426,165,368$。这样极大的增加了模型的灵活性。第二个好处是节省计算资源，因为每次只需要激活很少的Expert来参加计算，而不像transfomer那样所有的参数都参加计算。也就是说，MoE可以训练一个更大更多参数的模型，从而记住更多的知识，但是每次实际只有很少一部分参数参加计算。而且应为每个Expert是独立的模型，没有共享参数，所以他们可以并行进行计算。

MoE的架构见下图

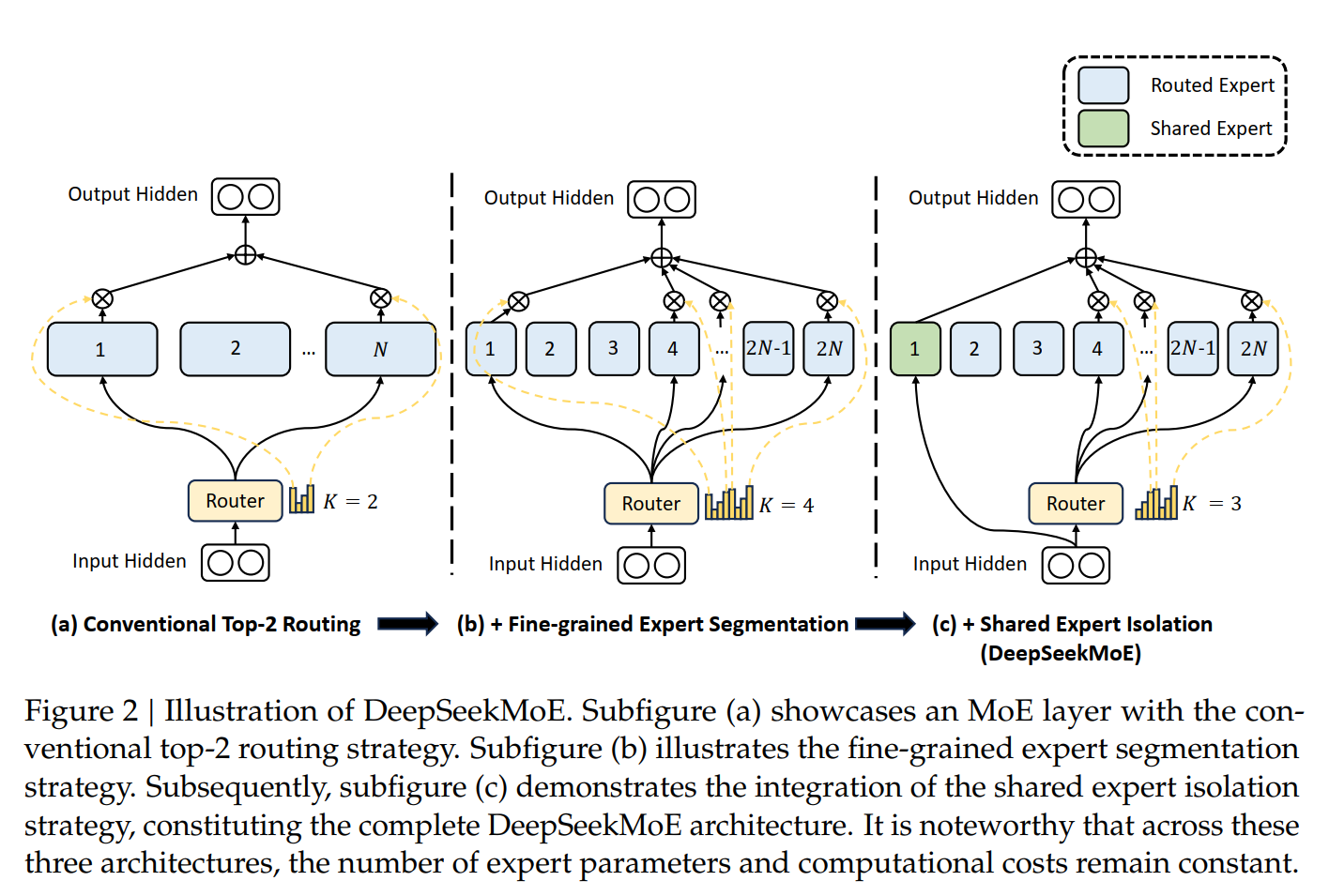
在DS的FFN里面，DeepSeekMoE在MOE的基础上更进一步：1）他们把Expert进一步细化，然后既有一些Expert用来做routing，具体地说，对routingd的Expert，预测只是route到这些Expert的某一些上面。同时，他们还有一些Expert是共享Expert，也就是说，在预测的时候，他们每次都是被使用。2）DS优化了Expert的选择，使用affinity score来选择专家。3）DS的Expert更finer，同时也更稀疏。这样进一步降低了运算成本。

DeepSeekMoE的架构见下图

假设每个Expert $i$ 的中心是 ${\mathbf{e}}_i$，首先计算 $\text{textcolor}blue{s}_{i,t}=\sigma ({\mathbf{u}}_t^{\mathrm{\top }}{\mathbf{e}}_i)$ 作为 token $t$ 与 Expert $i$ 的相似度： ${\mathbf{e}}_i$ 作为Expert $i$ 的中心向量，通过与token的输入 ${\mathbf{u}}_t$ 进行点积，再经过 sigmoid 计算出 token 对该Expert的 affinity，从而决定 token 是否被路由到该Expert。

$g_{i,t}^{\prime }$ 是Expert $i$的gating value，根据所有的Expert的 $s_{i,t}$的值，来选择最高的 $K_r$个。

然后算出这 $K_r$个Expert的权重 $\text{textcolor}blue{g}_{i,t}=\frac{g_{i,t}^{\prime }}{\sum _{j=1}^{N_r}{g}_{j,t}^{\prime }}$。尽管这儿的公式看分母是 $N_r$ 个 $g_{i,t}^{\prime }$ 相加，但是实际上有 $N_r-K_r$ 个为0.

最后得到新的output为 $\text{textcolor}blue{\mathbf{h}}_t^{\prime }={\mathbf{u}}_t+\sum _{i=1}^{N_s}{\text{FFN}}_i^{(s)}({\mathbf{u}}_t)+\sum _{i=1}^{N_r}{g}_{i,t}{\text{FFN}}_i^{(r)}({\mathbf{u}}_t)$. 注意的是，这里面从 $N_r$ 个Expert里面选择了 $K_r$个来进行计算，$K_r\ll N_r$，从而节约了大量的计算。同时，相比较于一般的MoE，DS使用了 $N_s$个 shared Expert，这些Expert参加所有的token的运算。通过引入共享专家，模型可以在不同任务之间共享通用知识，避免每个专家都独立学习相似的内容，从而减少了知识冗余。

Auxiliary-Loss-Free Load Balancing in DeepSeek-V3

实际运行的时候，可能会出现这种情况：模型的token大部分都是有某几个Expert来predict，剩下来的Expert使用率会比较少，导致Expert负载不均衡。以前的MOE使用auxiliary loss来让Expert负载均衡。通过惩罚imbalanced Expert utilization （加上更多的loss）来来达到均衡负载的目的。但是这样做有两个问题：1）Too strong auxiliary loss hurts model performance by interfering with learning objectives. 2）Difficult to tune: Balancing between efficiency and accuracy requires careful hyperparameter tuning.

DS提出了Auxiliary-Loss-Free Load Balancing来达到balanced routing of tokens to different Experts.具体的说实在gating function里面添加一个bias的项，通过bias的值来平衡Expert的调用。

具体的说，在计算权重$g_{i,t}^{\prime }$的时候，对每个token和Expert的affinity score都添加了一个bias $b_i$，变成$s_{i,t}+b_i\in \text{Topk}(\{s_{j,t}+b_j|1\le j\le N_r\},K_r)$, 当某个Expert $j$出现overload的时候，就把对应的$b_j$减小$\gamma$ 。这样的话新的$s_{j,t}+b_j$就会减小一点，这样的话 $\text{textcolor}blueTopk$ 个选择的时候这个Expert就会排名靠后一点，更可能不会被选中因为$g_{i,t}^{\prime }=0$。

Complementary Sequence-Wise Auxiliary Loss

DeepSeek-V3 主要依赖 Auxiliary-Loss-Free 负载均衡策略来确保 Experts 间的负载均衡。然而，为了防止单个序列内部的极端不平衡，DeepSeek-V3 还引入了 Complementary Sequence-Wise Auxiliary Loss. 通常MoE模型的负载均衡都在batch level进行，但是对一个batch的多个sequence，某个sequence 内部某些Expert可能用的很多，而其他Expert用的很少。DS的想法是要在每个sequence level，也尽可能的让Expert utilization均衡，负载不会过于集中或稀疏。同时该损失的强度非常低，以避免对模型性能产生负面影响。

下面我们主要来理解原文中的公式，为什么这个公式就能够均衡 Sequence level的Expert 负载。

$P_i$是看在 sequence 上面 Expert 的使用是不是比较均衡。如果不均衡的话，$P_i$的值就会比较大。具体原因：首先看$s_{i,t}^{\prime }$ 和 $P_i$。对归一化的affinity score $s_{i,t}^{\prime }=\frac{s_{i,t}}{\sum _{j=1}^{N_r}{s}_{j,t}}$, 计算Expert $i$ 在整个sequence (Sequence 的长度为 $T$) 上面的的平均得分 $P_i=\frac{1}{T}\sum _{t=1}^T{s}_{i,t}^{\prime }$: 如果Expert $i$ 在sequence的很多token $t$上被选中，那么对应的 $s_{i,t}$ 就会被其他的$s_{j,t}$大 ($s_{i,t}\gg s_{j,t}$ for $j\ne i$), 而 $s_{i,t}^{\prime }$ 是 $s_{i,t}$对所有的 Expert的归一化值，那么$s_{i,t}^{\prime }$就相应的比较大。而$P_i$是$s_{i,t}^{\prime }$在整个 sequence 上的平均值，所以它也会比较大。最后相对应的损失函数 ${\mathcal{L}}_{\text{Bal}}=\alpha \sum _{i=1}^{N_r}{f}_i{P}_i$ 就比较大。

$f_i$ 是 Expert $i$ 被使用的频率的归一化值。公式 $f_i=\frac{N_r}{K_{r}T}\sum _{t=1}^T\mathbb{1}(s_{i,t}\in \text{Topk}(\{s_{j,t}|1\le j\le N_r\},K_r))$ 统计了每个 Expert $i$ 在当前序列 $T$ 个token中被使用的频率 （$\sum _{t=1}^T\mathbb{1}(s_{i,t}\in \text{Topk}(\{s_{j,t}|1\le j\le N_r\},K_r))$），然后做了归一化 $\frac{N_r}{K_{r}T}$. 同样，如果 Expert $i$ 在这个 sequence 中被调用的次数很多，那么这个值也会更大。

最后，损失函数公式里的 $\alpha$ 是个取值很小的超参数。它的值很小是为了不过度影响主要训练目标。

2.2. Multi-Token Prediction (MTP)

DS还使用了MTP，而不是像一般的pre-training那样仅仅只预测 next token（2017的Attention文章就是只predict next token）。这有两个好处：1. 同时预测多个token可以提高data的使用效率。2. 让模型在准备representation的时候能够考虑的更长远。跟原始的MTP文章不同的是，DS不是同时predict $D$ 个token (输出一个 $D\times V$ 的矩阵， 其中 $V$ 是词表大小); 换个表达方式，对应的prediction 和损失函数是 $L_n=-\sum _t\log P_{\theta }(x_{t+n:t+1}\mid x_{t:1})$. DS是sequentially predict additional token。

MTP from Gloeckle et al. (2024), which is $D\times V$ 的矩阵

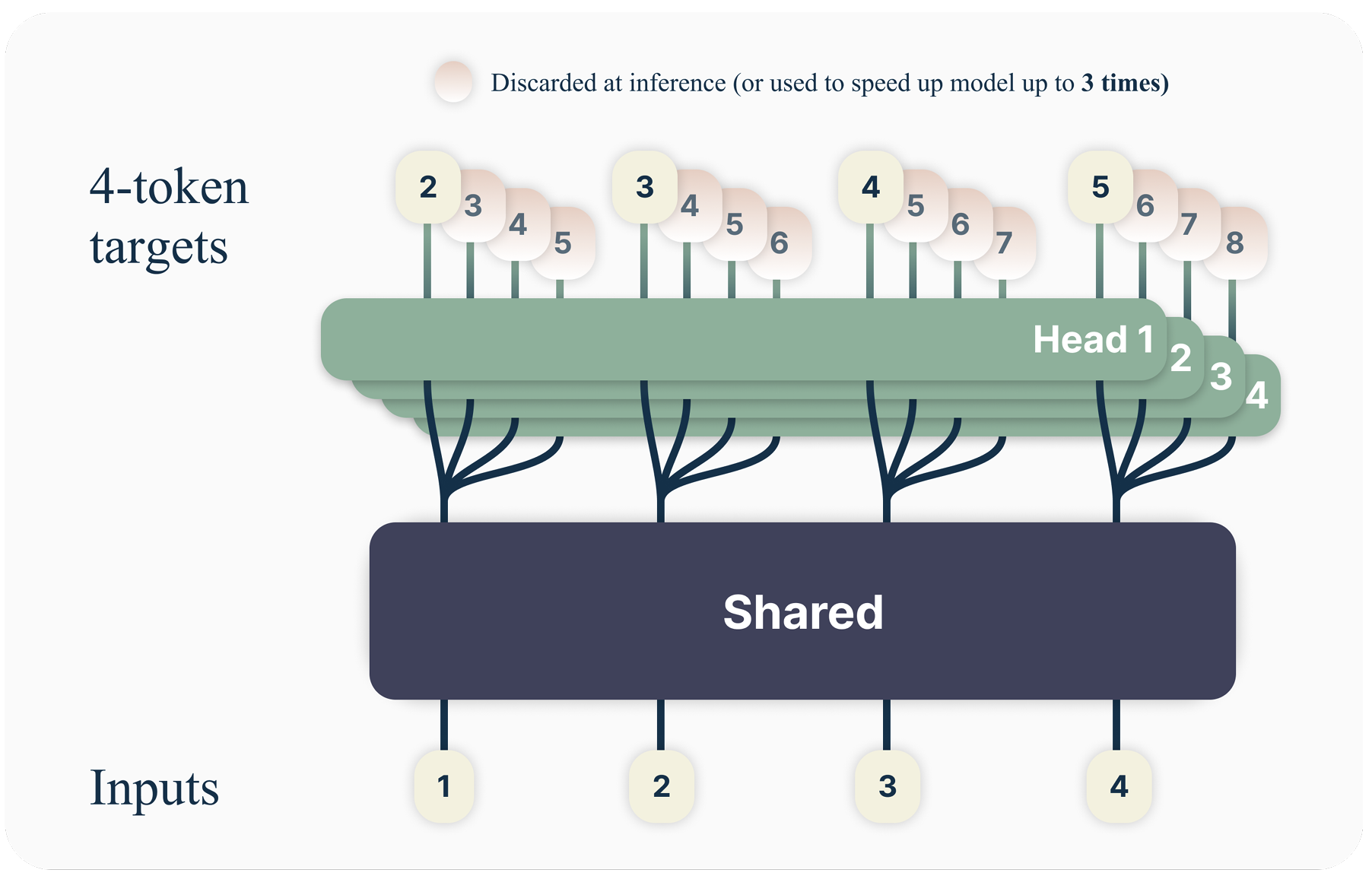
DS的MTP模块结构用一句话来简单概括就是：DS的MTP使用 $D$ 个sequential modules来预测 $D$ 个tokens。这 $D$ 个modules 共享 embedding $\text{Emb}(\cdot )$，共享输出头 $\text{OutHead}(\cdot )$ 。 第 $k$ 个token的 MTP 模块有一个专用的 transformer 块 ${\text{TRM}}_k(\cdot )$，以及一个投影矩阵 $M_k\in {\mathbb{R}}^{d\times 2d}$

DeepSeek V3 MTP: Use D MTP module and $k$-th module predict $k$-depth token

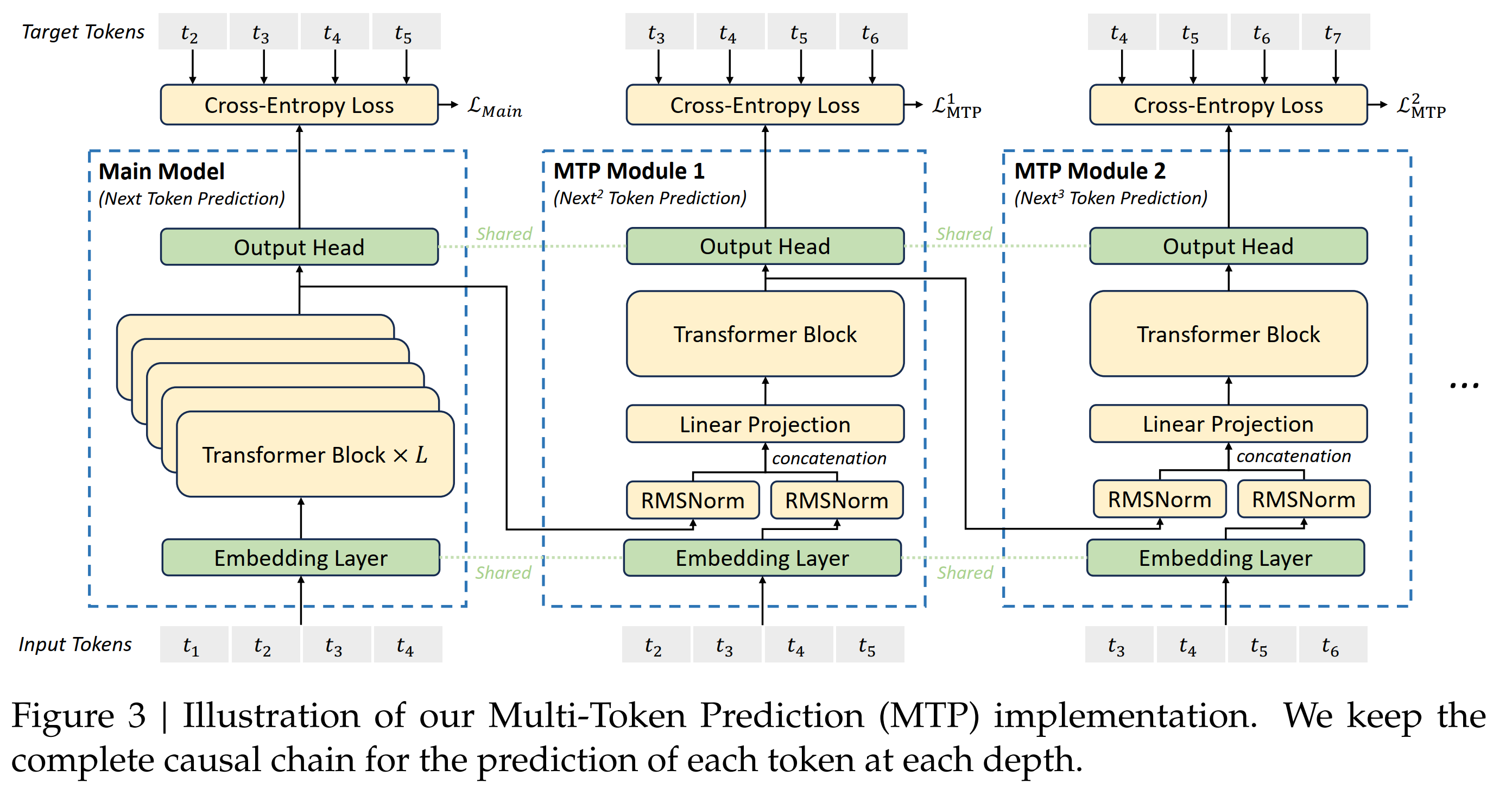
prediction：对于输入sequence的第 $i$ 个token $t_i$，在第 $k$ 个prediction depth (也就是下面要 predict $t_{i+k+1}$)，MTP module： 1）首先得到 $i$-th token 在第 $(k-1)$-th 深度的表示 ${\mathbf{h}}_i^{k-1}\in {\mathbb{R}}^d$， 以及第 $(i+k)$-th 个 token 的 embediding $Emb(t_{i+k})\in {\mathbb{R}}^d$； 2）然后把他们concat起来（长度为 $2d$），再通过 RMSNorm 和 投影矩阵 $M_k\in {\mathbb{R}}^{d\times 2d}$} 来生成新的表示 $h_i^{\prime k}=M_k[\text{RMSNorm}({\mathbf{h}}_i^{k-1});\text{RMSNorm}(Emb(t_{i+k}))]$；3）然后 ${\mathbf{h}}_i^{\prime k}$ 作为输入到第 $k$-th 个transformer 模块 ${\text{TRM}}_k(\cdot )$ ，生成当前深度的输出表示 ${\mathbf{h}}_{1:T-k}^k=TR{M}_k({\mathbf{h}}_{1:T-k}^{\prime k})$；最后使用 $\text{OutHead}$ 将 ${\mathbf{h}}_i^k$ 转换成预测概率 $p_{i+k+1}=OutHead({\mathbf{h}}_i^k)\in {\mathbb{R}}^V$。

我的理解：

1) 传统的next token prediction：$t_1$-> $h_1$ -> ${\hat{t}}_2$, $t_2$ -> $h_2$ -> ${\hat{t}}_3$, .... 也就是main model做的事情.

2) 在DS的 $k$-th MTP 模块中，模型会根据第 $(k-1)$-depth 的 MTP representation $h_i^{k-1}$ 和 token $t_{i+k}$ 的embedding来的到 $k$-depth 的representaion ${\mathbf{h}}_i^k$，从而更进一步来预测 $(k+1)$-th token。下面用 $k=1,2,3$ 作为例子来说明是怎么工作的。 具体来说, 对输入 token $i$ :

在 $k=1$ 的时候，先把 $t_i$ 的representaion $h_i^{k-1}=h_i^0$ （from main model） 和 token $t_{i+1}$ ($i+k=i+1$) 的embedding concat在一起得到 $h_i^{\prime 1}$，然后输入 $TR{M}_1$， 得到 ${\mathbf{h}}_{1:T-1}^1=TR{M}_1({\mathbf{h}}_{1:T-1}^{\prime 1})$， 最后得到token $t_{i+2}$ 的prediction 分布 $p_{i+2}$

在 $k=2$ 的时候，先把 $t_i$ 的representaion $h_i^{k-1}=h_i^1$ （from $k=1$ MTP module） 和 token $t_{i+2}$ ( $i+k=i+2$ ) 的embedding concat在一起得到 $h_i^{\prime 2}$，然后输入 $TR{M}_2$， 得到 ${\mathbf{h}}_{1:T-2}^2=TR{M}_2({\mathbf{h}}_{1:T-2}^{\prime 2})$， 最后得到token $t_{i+3}$ 的prediction 分布 $p_{i+3}$

在 $k=3$ 的时候，先把 $t_i$ 的representaion $h_i^{k-1}=h_i^2$ （from $k=2$ MTP module） 和 token $t_{i+3}$ ( $i+k=i+3$ ) 的embedding concat在一起得到 $h_i^{\prime 3}$，然后输入 ${\text{TRM}}_3$， 得到 ${\mathbf{h}}_{1:T-3}^3=TR{M}_3({\mathbf{h}}_{1:T-3}^{\prime 3})$， 最后得到token $t_{i+4}$ 的prediction 分布 $p_{i+4}$

MTP 的目标函数 对每个predict depth k，其损失函数仍然是cross-entropy，定义为 ${\mathcal{L}}_{\text{MTP}}^k$ = ${\mathcal{L}}_{\text{MTP}}^k$ = $\text{CrossEntropy}(P_{2+k:T+1}^k,t_{2+k:T+1})$ = $-\frac{1}{T}\sum _{i=2+k}^{T+1}\log p_i^k[t_i]$。其中 $T$ 是输入序列的长度, $t_i$ 是输入序列的第 $i$-th 个真实值, $p_i^k[t_i]$ 是第$k$-th 个 MTP 模块对 $t_i$ 的prediciton probability.

最终 MTP 的损失函数是对所有的预测深度 ($k$ 从1 到$D$) 的平均 乘以权重 $\lambda$ ，${\mathcal{L}}_{\text{MTP}}$ = $\frac{\lambda }{D}\sum _{k=1}^D{\mathcal{L}}_{\text{MTP}}^k$

从DS的paper公式25看，${\mathcal{L}}_{\text{MTP}}$ 只是 MTP 的损失函数。最终的损失函数应该还要加上 ${\mathcal{L}}_{\text{Main}}$。

MTP 在推理的时候怎么用呢？ MTP的主要目的是用来提高 main model的表现，在推理的时候，并不要使用MTP，而只是使用 main model来predict next token。

3. InfraStructures / 训练工程优化

3.1. Compure clusters

DS-V3 是在2048块H800上训练的，每个cluster有8块H800，nodes内通过NVLink和NVSwitch相连，nodes间通过InfiniBand来通信。

3.2. 训练框架

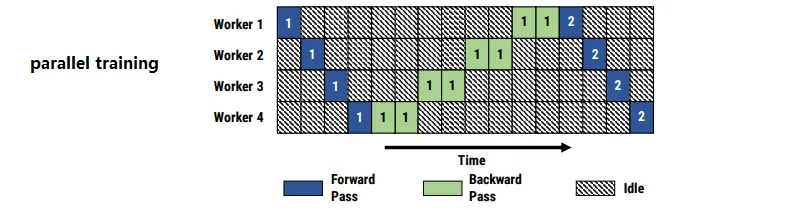
正常使用GPU进行训练的时候，有两个非常大的挑战：显存效率和计算效率，也就是显卡的显存和计算能力被使用了多少，有多少是浪费了。因为现在的模型太大，一张显卡或者一个cluster都放不下，所以通常需要把模型分散到不同的机器和显卡上。显卡，cluster组建集群参见kubernets的知识。为了把模型分散到不同的显卡上，通常有这么几个办法：1. Pipeline Parallelism / PP：这是对模型进行分割，对比较深的模型，模型的pipeline可以分到不同的显卡上。比如一个模型有32个transfomer，有八个显卡，那么可以每个显卡放4个，然后依次计算，这样可以使用micro-batch来充分的利用GPU。通常的PP会导致GPU闲置（见下图PP bubbles） 2. Tensor Parallelism / TP：这是对数据进行分割，对比较大的矩阵运算，可以分散到不同的显卡运算，这样既可以防止一张显卡容不下巨大的数据，也可以并行进行，加快速度。这些名字有时候不是很准确，其他还有Data Parallism, model parallelism. DS-V3因为有很多的Expert，所以他们还有 Expert Parallelism / EP。

PP bubbles:

setup	scenario	strategy
single node/multi-GPU	fits on single GPU	DistributedDataParallel or ZeRO
	doesn’t fit on single GPU	PipelineParallel, ZeRO or TensorParallel
	largest model layer doesn’t fit	TensorParallel or ZeRO
multi-node/multi-GPU	fast inter-node connectivity (NVLink or NVSwitch)	ZeRO or 3D parallelism (PipelineParallel, TensorParallel, DataParallel)
	slow inter-node connectivity	ZeRO or 3D parallelism (PipelineParallel, TensorParallel, DataParallel)

DS-V3是基于HAI-LLM训练框架。DS-V3通过16路PP，64路EP分布在8个节点上，以及ZeRO-1 DP.

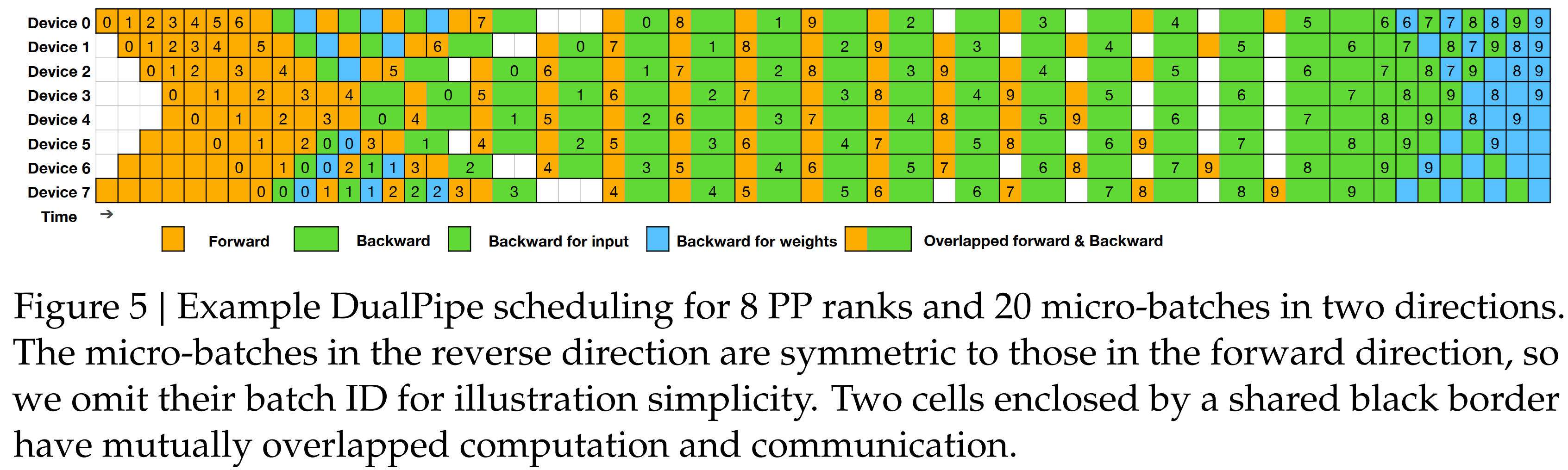
DS主要做了这三个工程优化：1. 设计了DualPile的办法来优化PP。DualPipe有更少的 pipeline bubbles（指GPU闲置），它将Forward和Backword过程的计算和通信阶段重叠起来，从而解决了跨节点专家并行性带来的沉重通信开销的挑战。2. 其次，开发了高效的 cross-node all-to-all 通信内核，充分利用 IB 和 NVLink 带宽，节省通信专用的 Streaming Multiprocessors (SMs)。最后，优化了训练过程中的内存占用，从而能够在不使用昂贵的 TP 的情况下训练 DeepSeek-V3。

3.2.1 DualPipe

在深度学习的大模型训练中，计算（Computation） 和 通信（Communication） 是两个关键环节。1. Computation： 主要指前向Forward 和 BackPropagation computation；2. Communication： 包括不同 GPU 或计算节点间的数据传输，如参数更新、梯度交换等。跨节点 Expert Parallelism 引入的通信开销导致计算与通信比率低效。DualPipe是一个双Pipeline的架构，在Pipeline的两端同时输入 Micro-Batches 的数据，这样 Forward 和 Backward 计算可以同步进行，减少 GPU 空闲时间。同时采用Computation与Communication重叠的策略，使得Forward 和 BackPropagation 的计算任务以及数据通信能够在时间轴上更紧密地交错。通过把Forward和Backward chunk成小块，然后调整GPU SMs的使用比例，一部分用于Computation，另一部分用于Communication。

DualPipe with less bubble

class DualPipeModel(nn.Module):
    def __init__(self, dim, rank, world_size):
        ...

    def forward_backward_pipeline(self, input_tensor):
        # 创建两个 CUDA 流，一个用于计算，一个用于通信
        compute_stream = torch.cuda.Stream()
        comm_stream = torch.cuda.Stream()

        # Forward Pass
        with torch.cuda.stream(compute_stream):
            attn_out = self.attention(input_tensor)
            mlp_out = self.mlp(attn_out)

        # Backward Pass
        with torch.cuda.stream(compute_stream):
            loss = mlp_out.sum()  
            loss.backward()

        # All-to-All Dispatch & Combine
        with torch.cuda.stream(comm_stream):
            tensor_to_send = input_tensor.clone()
            received_tensor = torch.zeros_like(input_tensor)
            # All-to-All 
            dist.all_to_all_single(received_tensor, tensor_to_send)

        # synchronize
        compute_stream.synchronize()
        comm_stream.synchronize()

        return received_tensor

3.2.2. Cross-Node All-to-All Communication

这一部分牵涉到更底层的工程细节，包括传说中的通过Nvidia的底层语言 PTX (Parallel Thread Execution) 来控制GPU的线程执行，减少通信对计算的影响，实现更高效的GPU利用，以及怎么充分利用集群的网络拓扑结构（IB & NVLink）。DS-V3 的原始paper里面也更多的是high-profile的描述而没有太多的细节。总体的思路是因为节点间IB的带宽比节点内NVLink的带宽要低，所以要想办法来合理分配通信路径，减少IB带宽的阻碍。

为了对 Cross-Node All-to-All Communication（包括 Dispatching 和 Combining）进行优化，DS设计了优化的网络拓扑结构（IB & NVLink）。在 dispatching 的时候，MOE gating algorithm 决定每个token 会被发送到哪些 Expert，每个 token 先通过 IB 发送到目标 node，然后再通过 IB-to-NVLink 将数据发送到最终的GPU。前面在模型架构已经提到，每个 token 最多发送给4个Node（NVLink的带宽为160GB/s，IB为50GB/s，大概是3.2倍，所以到了Node，token还能平均有3.2个Expert）。在 Combining 的时候反过来，每个 Expert 通过 NVLink 汇总数据的结果，然后通过 NVLink-to-IB 到 node汇总，IB 的接受和汇总同样由动态调整的warp处理。

3.2.3. Minimal Overhead

这一部分讲的怎么节省GPU内存的开支。第一个是在back propagaton的时候从新计算RMSNorm和升维投影，这样就不需要储存他们的值。第二个是咋Exponential Moving Average (EMA) 计算模型表现的时候，EMA参数放到CPU内存。第三个是在multi-token预测的时候，共享Embedding和Output Head的参数。

3.3. FP8 Training

首先加一个FP的知识，计算机用二进制表示浮点数，是分为正负号（Sign）、指数部分（exponent）、尾数部分（mantissa）三部分的，完整的表示为 $X=(-1{)}^s\times 2^E\times M$. 近似的可以认为：FP32和FP16比，FP越长，精度越高。在某些精度下已经等于0的数字，在更高的精度下就不是0，这样的话计算就不容易出现错误。但是更高的精度就需要更多的内存来存储，但是GPU通常内存有限。所以这也是一个需要优化的地方。

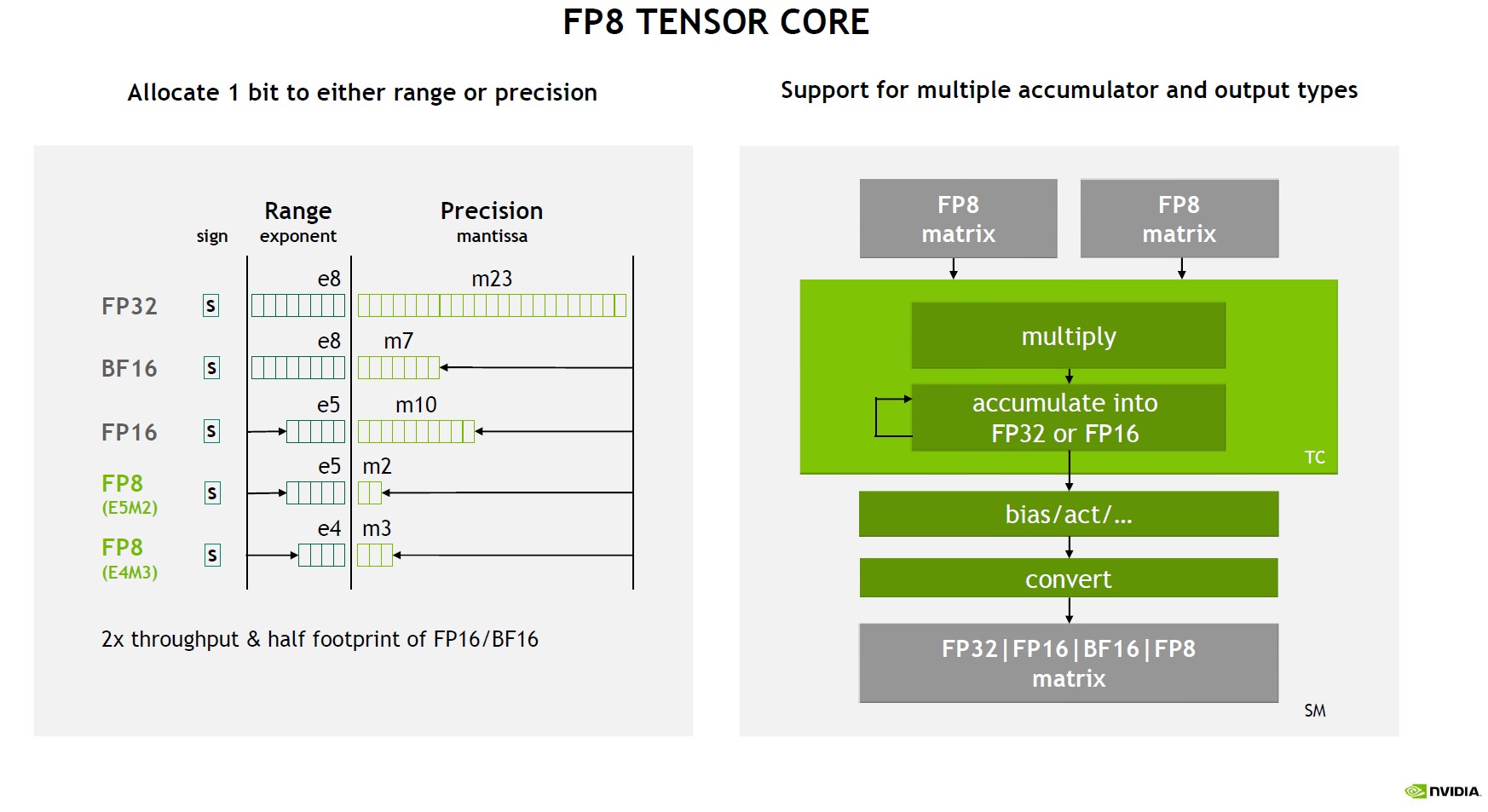Fig. NVIDIA FP8 Tensor Core

3.3.1. Mixed Precision Framework

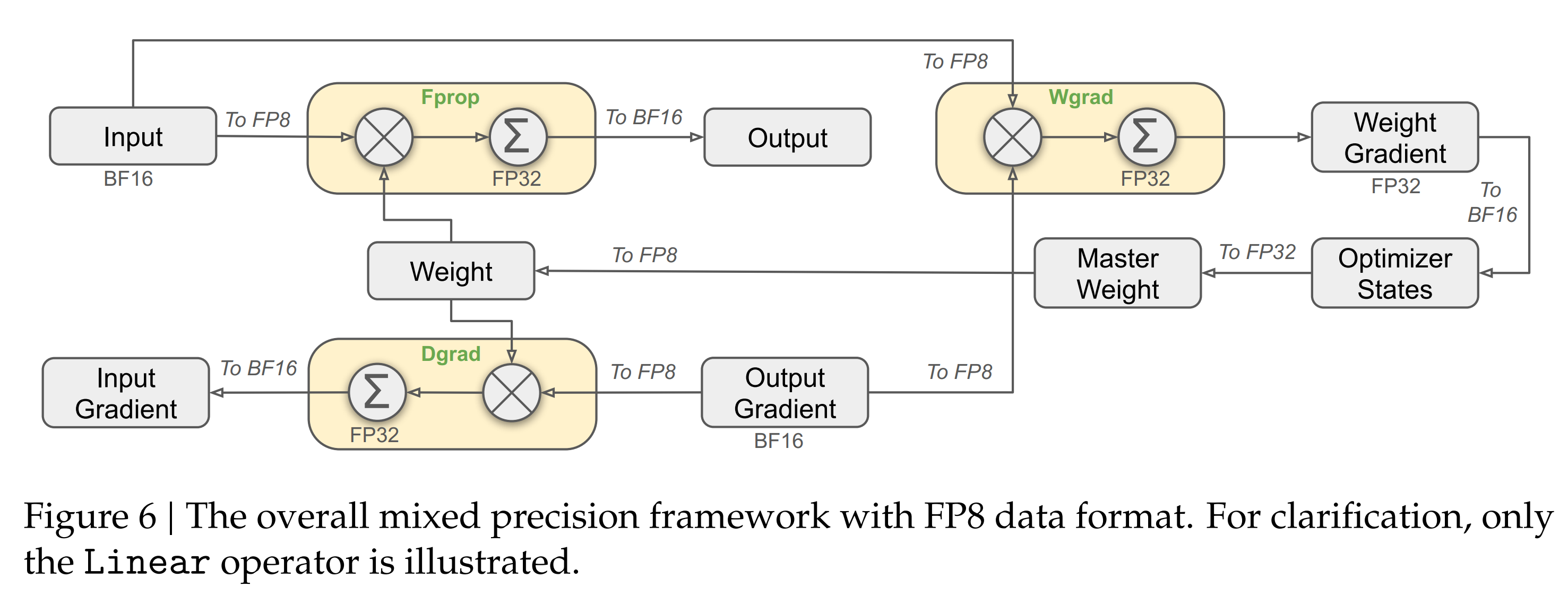
DS-V3 使用混合精度的FP8，大部分需要很多计算的地方都是FP8，但是在少量重要的操作上保留了原来的精度，具体见下图。1. 在GEMM矩阵相乘的时候，输入是FP8输出是BF16或者FP32. 在下图，在forward pass，activation backward pass和weight backward pass这几步矩阵相乘都是FP8的输入精度，理论上这样跟BF16比可以快一倍。在需要高精度的地方，比如embedding，output head，MOE gating module，normalizaiton，以及attention等等，仍然保持高精度。

Mixed Precision

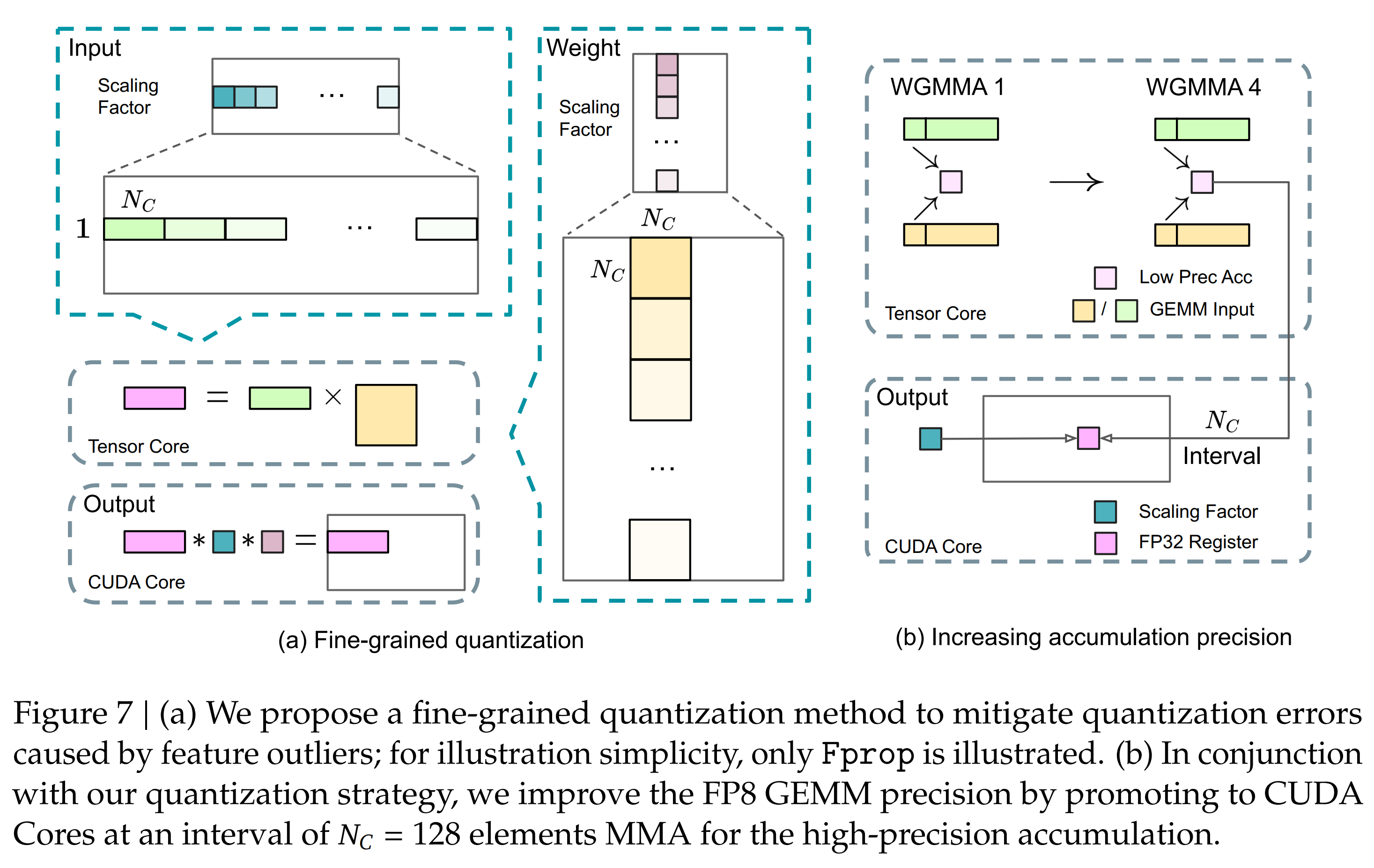
3.3.2. Improved Precision from Quantization and Multiplication

Fine-Grained Quantization 主要是为了解决低精度训练中 overflow 和 underflow 的问题。这些问题主要来源于 FP8 格式受限的动态范围，特别是 FP8 指数位减少导致的表示范围受限。为了解决这个问题，Fine-Grained Quantization 采用了一种更精细的量化方法，在更细粒度上进行 scaling：对activations，采用 $1\times 128\text{ tile-based scaling}$，每个tile分别计算scaling； 对于weights，采用 $128\times 128\text{ block-based scaling}$，每个bloack单独计算scaling factor。这样避免模型的参数会被outliers主导从而导致训练失败。在进行低精度FP8的矩阵运算 MMA (Matrix Multiply-Accumulate) 的时候，把计算的结果先累积在Tensor Core（FP8），当计算达到一定量的批次（$N_c$）的时候，将部分结果提升到 CUDA Core（FP32），这样在保持高throttle的同时，提高了最终的计算精度。

3.4. Inference and Deployment

Stay tuned!

Reference

1. DeepSeek-V3 Technical Report