pydata

Keep Looking, Don't Settle

Gradient Descent in solving linear regression and logistic regression

import numpy as np, pandas as pd
from matplotlib import pyplot as plt
import math

Gradient Descent is one of the optimization method by changing the parameters values in the negative gradient direction.

Let us assume the multi-variable function \(F(\theta|x)\) is differenable about \(\theta\). It is first order differentation to \(x\) is denoted as \(\triangledown F(\theta|x)\). To find the maximum(mimimum) of \(F(\theta|x)\) by iteration, we will let the parameter \(\theta\) change its value a little every time. The value changed along the gradient direction will be the fastest way to converge. So, from iteration \(\theta^{i}\) to iteration \(\theta^{i+1}\) we will let

$$ \theta^{i + 1} = \theta^{i} - \lambda \cdot \triangledown F\left(\theta^{i}|x\right)$$

where \(\lambda\) is called learning rate.

In the following two examples will be shown how gradient descent works to find the solution: one is for linear regression(which has closed-form solution) and the other is for logistic regression(which does not have closed-form solution).

alt text alt text

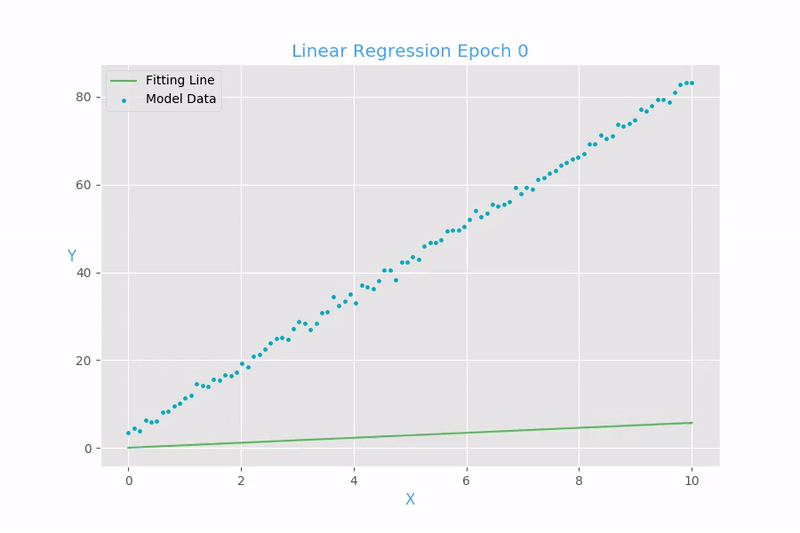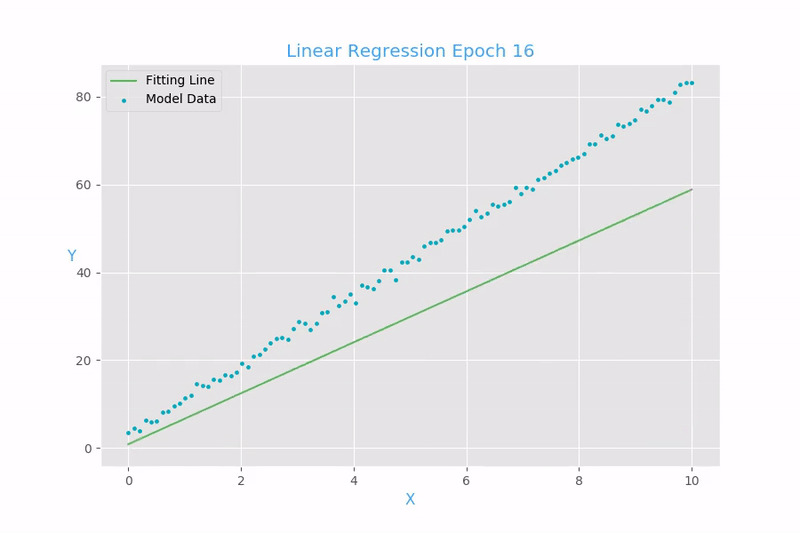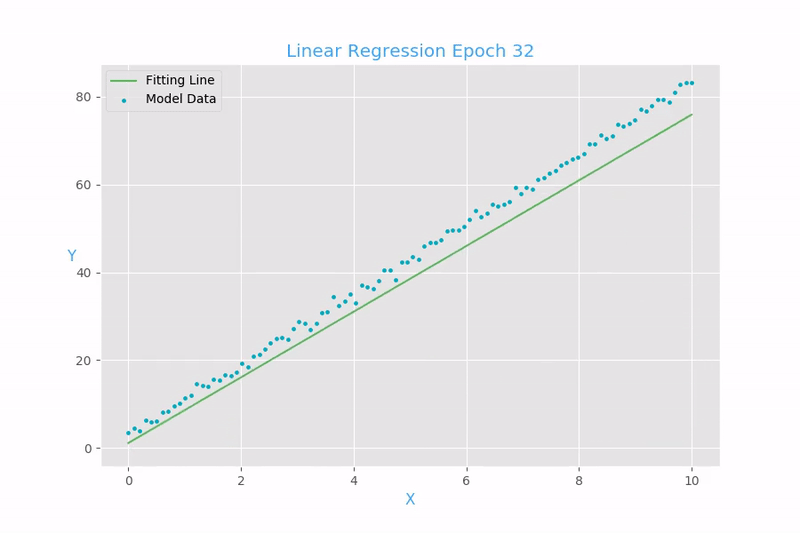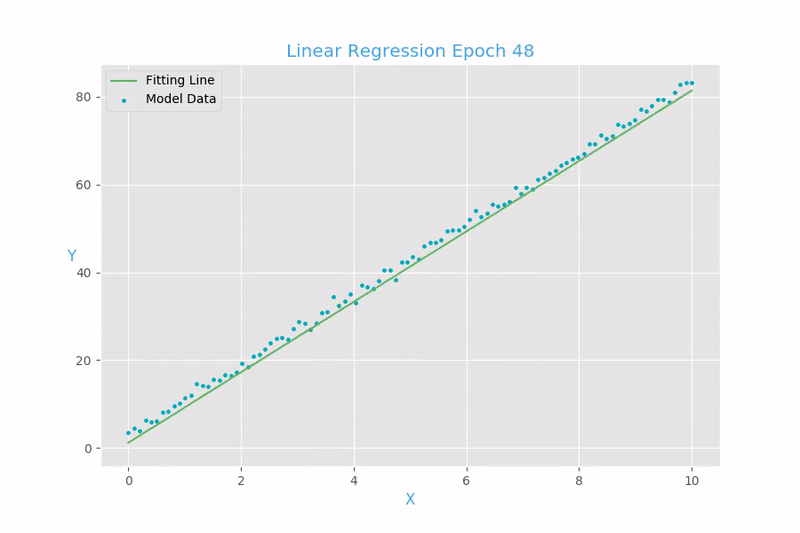
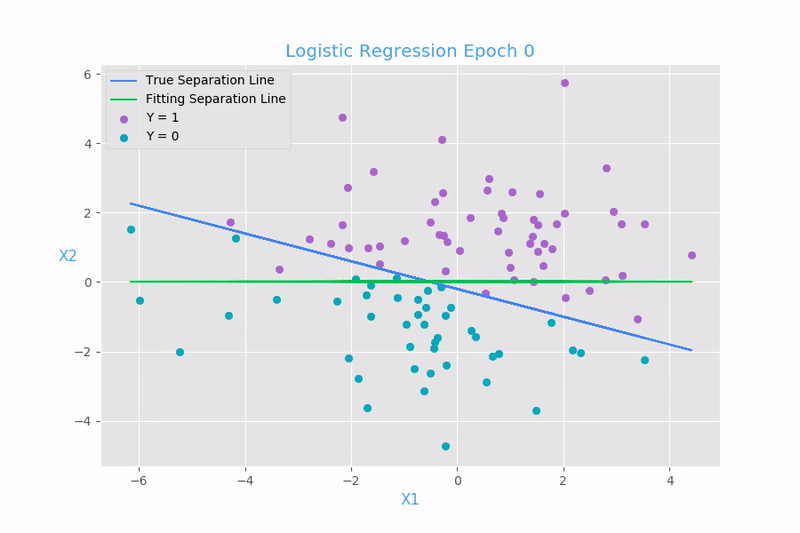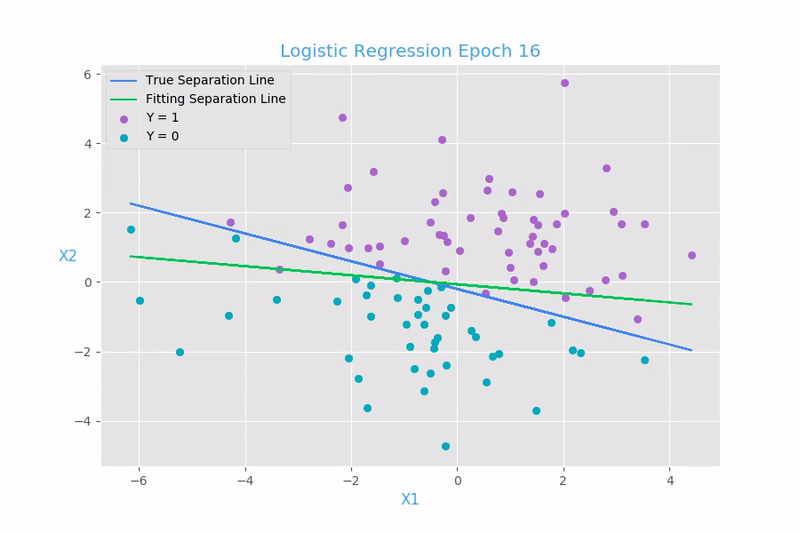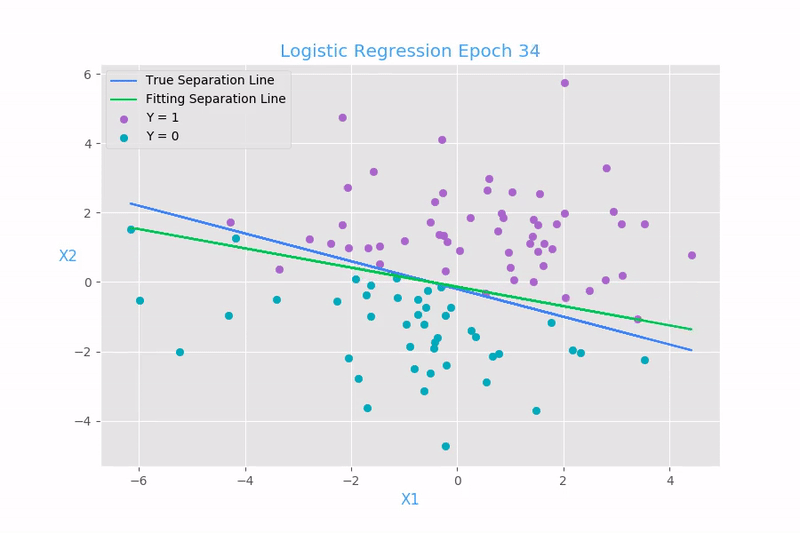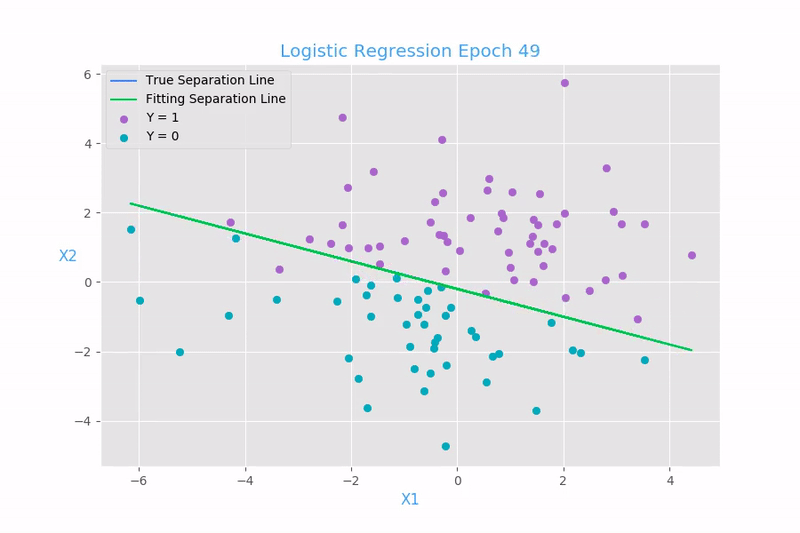
Example 1: Linear regression

A simple example of linear regression function can be written as

$$y_i = \alpha_0 + \alpha_1 \times x_i + \epsilon_i, ~~~ i = 1 \cdots n$$

we can write it in vector form as

$$ Y = XW + \epsilon $$

where

$$W = [\alpha_0, \alpha_1]'$$

The target is to minimize the Mean Square Error(mse) function defined as

$$MSE = \frac{1}{n}\sum_{i=1}^{n}\left(y_i - \alpha_0 - \alpha_1 \times x_i \right)^{2} = \frac{1}{n} (Y - XW)'(Y-XW)$$

We will call its main part Loss function :

$$ L = (Y - XW)'(Y-XW)$$

As introducted above, the gradient of the loss function to the parameter \(W\) is:

\begin{aligned} \frac{\partial L}{\partial W} & = \frac{\partial ( (Y - XW)'(Y-XW))}{\partial W} \\ & = \frac{\partial (Y'Y - 2W'X'Y + W'X'XW)}{\partial W} \\ &= -2X'(Y - XW) \end{aligned}

Now we will show how to use this gradient to find the final value of \(W\).

ns = 100
x = np.c_[np.ones(ns), np.linspace(0, 10, ns)]
y = x.dot([[3], [8]]) + np.random.normal(0, 1, ns).reshape(-1, 1)

def loss(w):
    e = y - x.dot(w)
    return e.T.dot(e)

The initial value of \(W\) will be

$$W_0 = [0, 0]'$$

For each loop,

$$W_{i+1} = W_i - \frac{\partial L}{\partial W} \times \lambda$$
w0 = np.array([0.0, 0.0]).reshape(2, 1)
learning_rate = 0.00001

i = 0
w = w0
while True:
    l1 = loss(w)
    dldw = -2 * x.T.dot(y - x.dot(w))
    w_new = w - dldw * learning_rate
    l2 = loss(w_new)
    w = w_new
    i += 1
    if i > 10000 or abs(l1 - l2) < 0.00001:
        break

print("The final value from gradient descent is alpha_0 = %.2f, alpha_1 = %.2f" %(w[0], w[1]))

The final value from gradient descent is alpha_0 = 2.41, alpha_1 = 8.09

alt text

For linear regression, we have the analytical solution(or closed-form solution) in the form:

$$W = (X'X)^{-1}X'Y$$

So the analytical solution can be calculated directly in python. The analytical solution is: constant = 2.73 and the slope is 8.02.

regres = np.linalg.inv((x.T.dot(x))).dot(x.T.dot(y))
print("The regression result is alpha_0 = {0:.2f}, alpha_1 = {1:.2f}".format(round(regres[0], 2), round(regres[1], 2)))

The regression result is alpha_0 = 2.43, alpha_1 = 8.09

Logistic Regression

Random variable \(Y\) has Bernoulli distribution:

$$ Y=\left\{ \begin{array}{ll} 1, \mbox{with probability} ~p\\ 0, \mbox{with probability} ~1 - p\\ \end{array} \right. $$

Here \(p\) is the function of \(X\) given parameters \(W\): \(p = p(X|W)\).

The logit function is

\begin{aligned} & ~~~~ \log \frac{p(X|W)}{1 - p(X|W)} = XW + \epsilon \\\\ & ==> p(X|W) = \frac{\exp(XW)}{ 1 + \exp(XW)} \triangleq h(W, X) \end{aligned}

here both \(X\) and \(W\) are vectors(shall be written as \(\vec{X}\) and \(\vec{W}\))

So the likelihood funciton can be written as

\begin{aligned} L(X, W) = \prod_{i=1}^{n} p\left(X_i|W\right)^{y_i} \left(1 - p\left(X_i|W\right)\right)^{(1 - y_i)} \end{aligned}

To max the likelihood function is the same as maximizing the log-likelihood funtion. The log-likelihood function is

\begin{aligned} LL(X, W) &= \log(L(X, W)) \\\\ &= \log\left(\prod_{i=1}^{n} p(X_i|W)^{y_i} (1 - p(X_i|W))^{(1 - y_i)}\right) \\\\ &= \sum_{i=1}^n \left[ y_i \log(p(X_i|W)) + (1 - y_i) \log(1 - p(X_i|W)) \right] \end{aligned}

from this we can get the gradient of \(W\) is

\begin{aligned} \frac{\partial LL(X, W)}{\partial W} = \sum_{i=1}^n \left( h(W, X_i) - y_i \right) X_i \end{aligned}

where

$$ h(W, X_i) = \frac{\exp(X_i W)}{ 1 + \exp(X_i W)} $$

Next an example is shown how to use gradient descent to find the solution of \(W\) to maximize the likelihood function.The link function is of the form:

$$\log \frac{p}{1-p} = \beta_0 + \beta_1 x_1 + \beta_2 x_2$$
w = np.array([1, 2, 5]).reshape(3, 1)
np.random.seed(99)
x = np.c_[np.ones(100).reshape(100, 1), np.random.normal(0, 2, 200).reshape(100, 2)]
s = x.dot(w) + np.random.normal(0, 1, 100).reshape(100, 1) 
p = np.exp(s) / (1 + np.exp(s)) 
y = np.random.binomial(1, p).reshape(100, 1)

def sgd(x, y, w):
    expval = np.exp(x[:, :].dot(w))
    return np.sum([expval / (1 + expval) - y] * x, axis = 1).reshape(3, -1)

w0 = np.zeros(3).reshape(3, 1)
learning_rate = 0.01

i = 0
w = w0
while True:
    dlldw = sgd(x, y, w)
    w_new = w - dlldw * learning_rate
    i += 1
    if i > 1000 or sum((w - w_new)**2)<0.00001:
        break
    w = w_new

print("The fitting result from gradient descent is beta0 = %.2f, beta1 = %.2f, beta2 = %.2f" %(w[0], w[1], w[2]))

The fitting result from gradient descent is beta0 = 1.09, beta1 = 1.82, beta2 = 5.20

plt.scatter(x[y.reshape(100, ) ==1, 1], x[y.reshape(100, ) ==1, 2], color = "#aa66cc", label = "Y = 1")
plt.scatter(x[y.reshape(100, ) ==0, 1], x[y.reshape(100, ) ==0, 2], color = "#00aabb", label = "Y = 0")
plt.plot(x[:, 1], -0.2 - 0.4 * x[:, 1], color = "#4285F4", label = "True Separation Line")
plt.plot(x[:, 1], -x[:, :2].dot(w[:2, 0] / w[2, 0]), color = "#00C851", label = "Fitted Separation Line")
plt.xlabel("X1", color = '#42a5f5', size = "18")
h = plt.ylabel('X2', color = '#42a5f5', size = "18")
h.set_rotation(0)
plt.title("Logistic Regression Separation Line", color = "#42a5f5", size = "18")
plt.legend(loc=2)

png

alt text

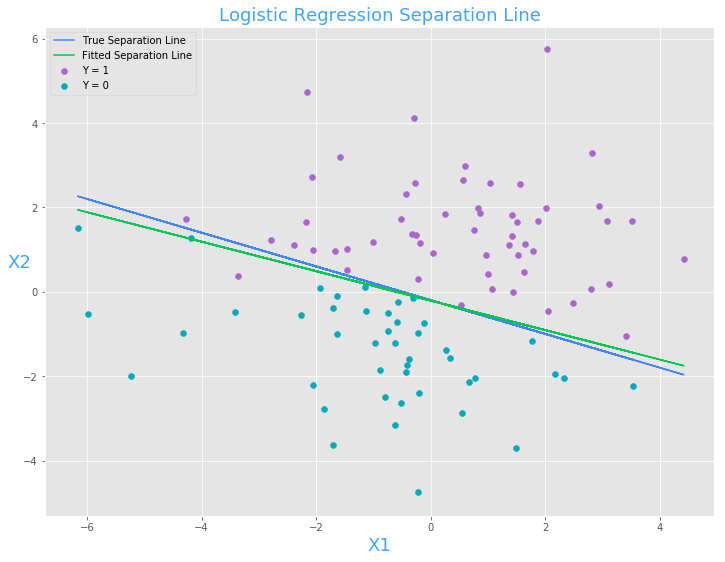
The same as linear regression, we can use sklearn(it also use gradient method to solve) or statsmodels(it is the same as traditional method like R or SAS did) to get the regression result for this example:

from sklearn.linear_model import LogisticRegression
logfit = LogisticRegression()
logfit.fit(x, y)
sklearn_w = logfit.coef_[0]
print("The fitting result from gradient descent is beta0 = %.2f, beta1 = %.2f, beta2 = %.2f" %(sklearn_w[0], sklearn_w[1], sklearn_w[2]))

# import statsmodels.formula.api as smf
# import statsmodels.api as sm
# import pandas as pd
# mydata = pd.DataFrame(np.c_[x, y], columns = ["const", "x1", "x2", "y"])
# mod1 = smf.glm(formula = "y ~ x1 + x2", data=mydata, family=sm.families.Binomial()).fit()
# print (mod1.params)

The fitting result from gradient descent is beta0 = 0.27, beta1 = 0.95, beta2 = 2.72

bootstrap color hex value